
The plastic material in RecurDyn is a J2 plasticity formulation, which is also known as Von-Mises plasticity. This is a small-strain plasticity formulation that is strain-rate independent. It is appropriate for metals at low strain rates. In the elastic range, it is equivalent to the isotropic material. The J2 plastic material in RecurDyn uses an associative flow model.
Plastic materials can be assigned to FFlex bodies that contain hexa-dominant elements (Solid4, Solid5, Solid6 and Solid8) and Shell4 elements.
Plastic materials make to consider the permanent deformation caused by the load over the yield stress. When comparing the elastic materials to the plastic material as shown in Figure 1, the different characteristics of plastic material can be shown easily.

Figure 1 Strain vs. stress curves of elastic and plastic materials
Two kinds of work hardening are modeled in RecurDyn’s plastic material: isotropic hardening and kinematic hardening. All plastic materials require isotropic hardening. Optionally, they can also have the kinematic hardening.
•3 types for Isotropic Hardening exist:
•Multilinear (Default)
•Bilinear
•Nonlinear
Figure 2 shows the characteristic of 3 types for Isotropic Hardening of the relationship of strain vs. stress.
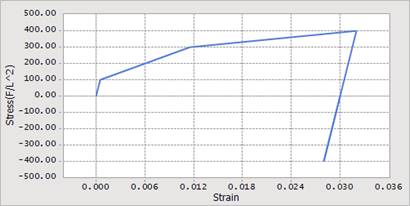
< Multi-linear relationship >
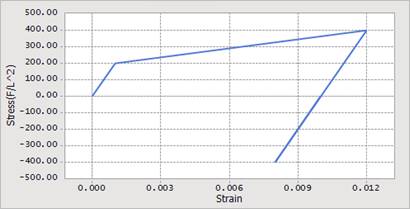
< Bi-linear relationship >

< Non-linear relationship >
Figure 2 Strain vs. stress curves of 3 types of Isotropic Hardening
There is only one type of Kinematic Hardening: bilinear kinematic hardening. This kinematic hardening model can be used with any of the isotropic hardening models.
The parameters of the plastic material are defined in the following dialog box:

Figure 3 Multi-linear isotropic hardening input

Figure 4 Bilinear / Nonlinear isotropic hardening input
•The Elastic Properties of the material are defined by the fields
•Young’s Modulus
•Density
•Damping Ratio
•Shear Modulus
•Poisson’s Ratio
The interpretation of these fields is identical to the isotropic elastic material. Please chick here for more information on these fields.