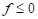 :
:
The interpretation of the hardening input can be seen from the equation that defines the state of plastic material.
This function is the yield function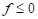 :
:

Where,
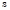 is the deviatoric stress
is the deviatoric stress
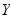 is the yield stress
is the yield stress
 is the back stress
is the back stress
If 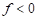 , the material is in an elastic
state. If
, the material is in an elastic
state. If 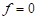 , the material is in a plastic
state.
, the material is in a plastic
state.
And then if 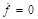 and the deviatoric strain rate
is not zero (
and the deviatoric strain rate
is not zero ( ), then the plastic flow is
occurring.
), then the plastic flow is
occurring.
Note that it is not possible for 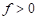 . The deviatoric stress is given
by
. The deviatoric stress is given
by

Where,
 is the shear modulus
is the shear modulus
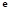 is the total deviatoric
strain
is the total deviatoric
strain
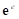 is the elastic deviatoric
strain
is the elastic deviatoric
strain
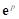 is the plastic deviatoric
strain
is the plastic deviatoric
strain
The deviatoric strains satisfy the equation:

The relationship between the total deviatoric strain 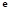 and the true strain
and the true strain 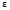 is:
is:
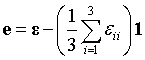
Where 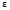 is the true strain,
measured using small strain theory, and
is the true strain,
measured using small strain theory, and 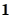 is the 3x3 identity
matrix.
is the 3x3 identity
matrix.
The yield stress 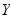 implements the isotropic
hardening. If the isotropic hardening is present,
implements the isotropic
hardening. If the isotropic hardening is present, 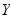 will increase as plastic flow
occurs. If no isotropic hardening is present, then
will increase as plastic flow
occurs. If no isotropic hardening is present, then 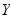 is a constant and does not
change with plastic flow. The exact form of
is a constant and does not
change with plastic flow. The exact form of 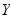 depends on the type of
isotropic hardening that is chosen. In all 3 types of isotropic hardening,
depends on the type of
isotropic hardening that is chosen. In all 3 types of isotropic hardening, 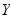 is a function of
is a function of 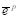 , where
, where 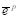 is defined by the differential
equation:
is defined by the differential
equation:
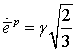
Where, 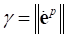
and for any arbitrary 3x3 matrix 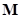 :
:

The back stress  implements the kinematic
hardening. It permits the yield surface defined by
implements the kinematic
hardening. It permits the yield surface defined by 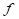 to shift without changing its
size. This is easiest to understand with a 1-dimensional example. If uni-axial
specimen is stretched, then the kinematic hardening would allow the yield point
in tension to rise and simultaneously for the yield point in compression to
decrease in magnitude.
to shift without changing its
size. This is easiest to understand with a 1-dimensional example. If uni-axial
specimen is stretched, then the kinematic hardening would allow the yield point
in tension to rise and simultaneously for the yield point in compression to
decrease in magnitude.
In 3-dimensional plastic deformation, the back stress  allows for the center of the
plastic yield surface to shift in the direction of plastic flow.
allows for the center of the
plastic yield surface to shift in the direction of plastic flow.