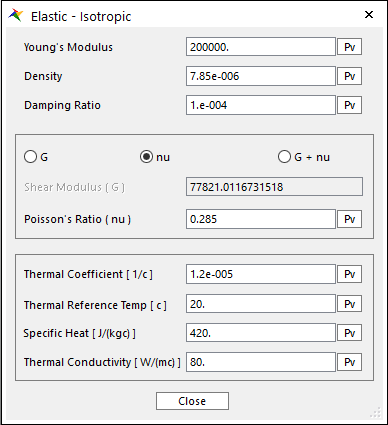
Figure 1 Elastic – Isotropic(Linear) dialog box
•Young’s Modulus, Density, and Damping Ratio are set.
•Damping Ratio
o MFBD system equation is composed of mass matrix, damping matrix and stiffness matrix. Generally, mass matrix and stiffness matrix can be evaluated using finite element formulation but damping matrix cannot be evaluated using it. So, damping ratio, which is a ratio between stiffness matrix and damping matrix, is used to evaluate damping matrix.
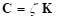
where:
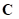: Damping Matrix
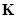: Stiffness Matrix
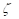: Damping Ratio
NOTE
The Damping Ratio doesn’t mean an actual damping divided by a critical damping. The Damping Ratio is related the Rayleigh Damping of the structural dynamics. The Rayleigh Damping means that the damping matrix is defined a linear combination of Mass and Stiffness matrices as following equation.
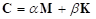
The alpha (a proportional coefficient of Mass matrix) is always set zero, and the beta (a proportional coefficient of Stiffness matrix) is related the Damping Ratio for the RecurDyn/FFlex.
•In general, Shear Modulus is calculated from Young’s Modulus and Poisson’s Ratio in the isotropic material.
•Using this relation, Shear Modulus (G) and Poisson’s Ratio (nu) are set from the follow options, G, nu, and the G+nu.
•G
o If Shear Modulus (G) is set, Poisson’s Ratio (nu) is calculated.
o If the values of Poisson’s Ratio are not in the range of 0 to 1, then the warning message will be seen for the wrong material property.
•nu
o If Poisson’s Ratio is set, then the Shear Modulus(G) is calculated.
•G + nu
o The values of Shear Modulus (G) and Poisson’s Ratio (Nu) are set.
o But If the relation of Shear Modulus (G), Poisson’s Ratio (Nu), and Young’s Modulus is not met, the warning message will be seen for the wrong material property.
•Thermal Coefficient: The ratio between the original length and stretched length by the temperature. It is the material property.
•Thermal Reference Temp: The reference temperature is user-defined value. The difference between current temperature and reference temperature occur the thermal deformation.
•Stress-strain matrix (E)
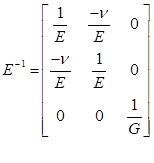
•Specific Heat: The specific heat capacity of a substance is the heat capacity of a sample of the substance divided by the mass of the sample. This value is used for making capacity matrix for conduction analysis.
•Thermal Conductivity: The thermal conductivity of a material is a measure of its ability to conduct heat. This value is used for making conductivity matrix for conduction analysis.