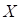 is a random variable and
is a random variable and 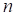 observations of
observations of 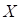 are available. We can
evaluate the mean value of
are available. We can
evaluate the mean value of 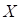 as
as
Suppose that 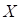 is a random variable and
is a random variable and 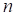 observations of
observations of 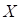 are available. We can
evaluate the mean value of
are available. We can
evaluate the mean value of 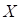 as
as
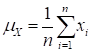
This is a measure of central tendency in data, which is known as the 1st central moment. Also, a measure of spread in the data about the mean value can be evaluated as
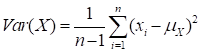
This is known as the variance of 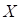 and the 2nd central moment. In order
to avoid the dimension problem between the mean and the variance, the following
standard deviation is widely used.
and the 2nd central moment. In order
to avoid the dimension problem between the mean and the variance, the following
standard deviation is widely used.
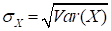
Although the standard deviation is represented in the same units as the mean value, its value does not clearly indicate the degree of dispersion in the random variables, without referring to the mean value. Thus, a dimensionless value is widely used to express the dispersion, which is called the coefficient of variance (COV).
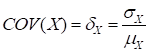
A smaller value of COV represents a smaller amount of uncertainty in the variable and larger amount indicates a larger amount of uncertainty.