Beta Distribution
The beta distribution is a useful distribution used when the
upper and lower bounds of a random variable are defined as 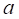 and
and 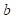 . Since the normal distribution is
defined between
. Since the normal distribution is
defined between  and
and
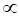 , the log-normal distribution
is defined between 0 and
, the log-normal distribution
is defined between 0 and 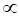 , it
is sometimes difficult to apply to the engineering random variable defined only
in the given upper and lower limit range. The probability density function of
the beta distribution is
, it
is sometimes difficult to apply to the engineering random variable defined only
in the given upper and lower limit range. The probability density function of
the beta distribution is
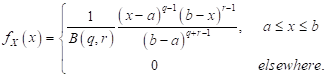
where 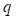 and
and 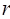 are the parameters for distribution
and
are the parameters for distribution
and 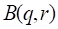 is the beta
function. The parameters
is the beta
function. The parameters 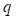 and
and 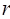 have the following relationship with
Mean and Standard Deviation:
have the following relationship with
Mean and Standard Deviation:
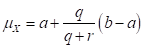 and
and
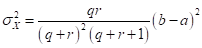
Then, if we know mean, standard deviation and the
distribution parameters 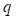 and
and 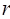 , we can compute the lower and upper bounds
as
, we can compute the lower and upper bounds
as
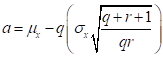 and
and
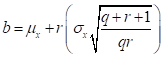
When 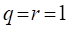 , the beta distribution becomes the
uniform distribution.
, the beta distribution becomes the
uniform distribution.
Reference
1. Rao, S.S., Reliability-Based
Design, McGraw-Hill, Inc., New 0York, 1992.
2. Haldar, A, and Mahadevan, S.,
Probability, Reliability, and Statistical methods in Engineering Design, John
Wiley & Sons, Inc., 2000.
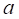 and
and 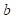 . Since the normal distribution is
defined between
. Since the normal distribution is
defined between  and
and
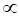 , the log-normal distribution
is defined between 0 and
, the log-normal distribution
is defined between 0 and 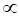 , it
is sometimes difficult to apply to the engineering random variable defined only
in the given upper and lower limit range. The probability density function of
the beta distribution is
, it
is sometimes difficult to apply to the engineering random variable defined only
in the given upper and lower limit range. The probability density function of
the beta distribution is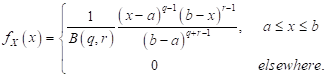
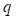 and
and 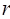 are the parameters for distribution
and
are the parameters for distribution
and 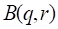 is the beta
function. The parameters
is the beta
function. The parameters 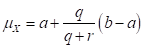 and
and
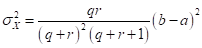
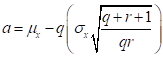 and
and
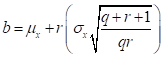
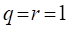 , the beta distribution becomes the
uniform distribution.
, the beta distribution becomes the
uniform distribution.