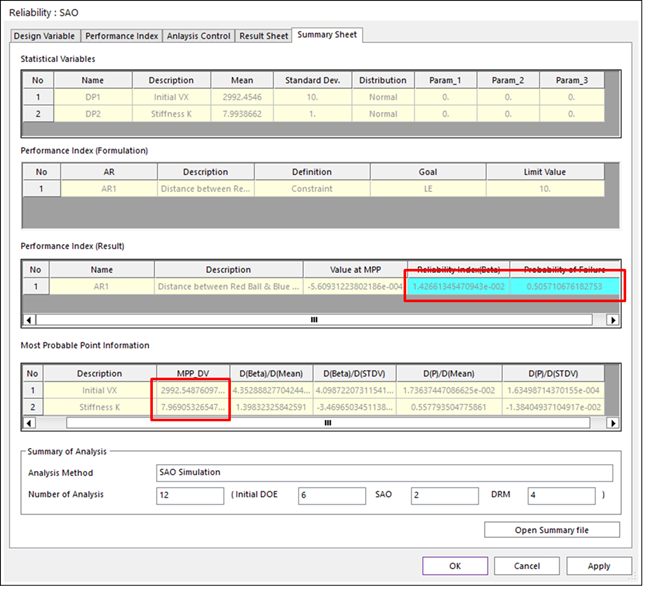
Check ‘Summary Sheet’ in the ‘Reliability: SAO’ dialogue. Then, you can see the reliability analysis result. ‘Statistical Variables’ lists the random constant information. Param_1 ~ Param_3 are the statistical values for defining the probabilistic distributions, which are internally evaluated from the given information such as mean, standard deviation and distribution type. ‘Performance Index (Formulation)’ lists the limit state function formulation.
‘Performance Index (Result)’ list the reliability analysis results, which should be nearly zero at MPP. Reliability index denote the minimum distance from mean value to MPP. The probability of failure is the modified failure by using DRM. In the convergence history, AFORM gave ‘0.5106’. The modified failure is ‘0.5057’, which is more accurate result. If you need the detailed theory, you can see Reliability Analysis.
‘Most Probability Point Information’ gives a design guide. First, it shows MPP location (2992.54876, 7.969). D(Beta)/D(Mean) represents the design sensitivity values. If this value is positive, then the reliability index will be increased by increasing mean value. Also, D(P)/D(Mean) value is the derivative of failure probability with respect to mean value. Figure 1 shows that DP2 is more sensitive than DP1.
Finally, total number of analyses is summarized. The SAO method uses only 12 evaluations to find the failure probability of system. The SAO based AFORM used 8 evaluations and DRM2 used 4 evaluation. Next, by comparing the results of Monte-Carlo simulation, you can see SAO approach is most efficient.

Figure 1 Summary Sheet