A mechanical or structural component is considered to be safe
and reliable when the strength or resistance of component exceeds the value of
load acting on it. Thus, the computation of the reliability of the component
requires the knowledge of the random nature of the strength(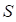 ) and the load(
) and the load( ). If the probability density functions of
). If the probability density functions of
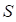 and
and  are known to be
are known to be 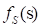 and
and  as shown in Figure 1, then the reliability
of the component can be evaluated by constructing integral equations. If
as shown in Figure 1, then the reliability
of the component can be evaluated by constructing integral equations. If 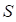 and
and  are independent, then the
interference area shown in Figure 1, between the probability density functions
of
are independent, then the
interference area shown in Figure 1, between the probability density functions
of 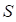 and
and  , gives a measure of the probability of
failure. The reliability of a component
, gives a measure of the probability of
failure. The reliability of a component 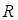 is given by
is given by

where 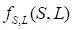 is the joint density function of
is the joint density function of 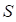 and
and  . In certain cases, such as the cases in
which
. In certain cases, such as the cases in
which 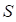 and
and  follow normal, lognormal, exponential
distributions, the integral equation can be reduced to a simple form. However,
in a more general case, the reliability of the component can be found only by
evaluating the integrals numerically. Two methods of evaluating the reliability
of mechanical components are discussed in this chapter.
follow normal, lognormal, exponential
distributions, the integral equation can be reduced to a simple form. However,
in a more general case, the reliability of the component can be found only by
evaluating the integrals numerically. Two methods of evaluating the reliability
of mechanical components are discussed in this chapter.
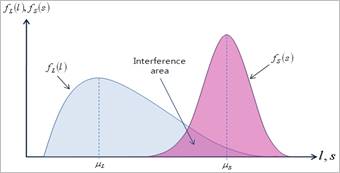
Figure 1 Graphical representation for reliability
analysis
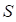 ) and the load(
) and the load( ). If the probability density functions of
). If the probability density functions of
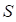 and
and  are known to be
are known to be 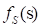 and
and  as shown in Figure 1, then the reliability
of the component can be evaluated by constructing integral equations. If
as shown in Figure 1, then the reliability
of the component can be evaluated by constructing integral equations. If 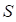 and
and  are independent, then the
interference area shown in Figure 1, between the probability density functions
of
are independent, then the
interference area shown in Figure 1, between the probability density functions
of 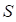 and
and  , gives a measure of the probability of
failure. The reliability of a component
, gives a measure of the probability of
failure. The reliability of a component 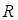 is given by
is given by
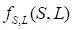 is the joint density function of
is the joint density function of 