Roller and Sheet Interactions

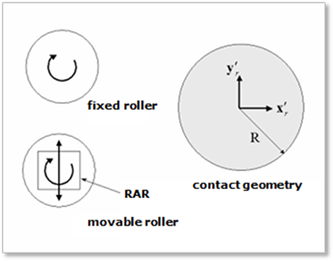
Figure 1 Definition of rollers
There are two types of rollers.
•One is a fixed roller with one rotational degree of freedom.
•The fixed roller is linked to the ground with a revolute joint.
•The other is a movable roller that has two degrees of freedom for both translational and rotational motion.
•The movable roller is linked to a rotational axis retainer (RAR) with a revolute joint.
•The retainer is linked to the ground with a translational joint.
The contact geometry of rollers is described as a circle as shown in Figure 1.
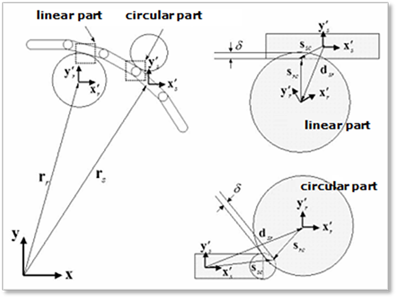
Figure 2 Sheet and roller interaction
The contact between a roller and a sheet has two types, as shown in Figure 2.
•One is a roller contact to the linear part of the sheet segment.
•The other is a roller contact to the circular ends of the sheet segment.
The relative displacement between a rigid segment and a roller can be computed according to the following equation.
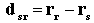 (1)
(1)
where, 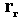 and
and 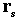 are the
center position vectors of the roller and the rigid segment, respectively. The
vector of
are the
center position vectors of the roller and the rigid segment, respectively. The
vector of 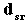 is projected by the body
reference frame of a contacted rigid segment and the resultant displacement can
be represented as follows.
is projected by the body
reference frame of a contacted rigid segment and the resultant displacement can
be represented as follows.
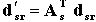 (2)
(2)
where, 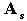 is the orientation matrix of a
rigid segment. From Eq. (2), if the absolute value of x component of
is the orientation matrix of a
rigid segment. From Eq. (2), if the absolute value of x component of 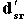 is less than
is less than 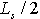 , the roller will contact the linear
part of a sheet. If not, the roller is contacting the circular ends of the
segment.
, the roller will contact the linear
part of a sheet. If not, the roller is contacting the circular ends of the
segment.
In a linear part contact, the contact penetration is determined as follows.
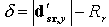 (3)
(3)
where, 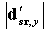 and
and 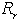 are the y
component of the vector of
are the y
component of the vector of 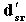 and the radius of a contacted
roller, respectively. The contact positions from segment and the roller center
can be computed as follows.
and the radius of a contacted
roller, respectively. The contact positions from segment and the roller center
can be computed as follows.
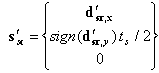 (4)
(4)
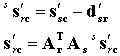 (5)
(5)
where, 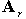 is the orientation matrix of a roller. The
relative velocity at the contact point can be determined as follows.
is the orientation matrix of a roller. The
relative velocity at the contact point can be determined as follows.
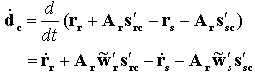 (6)
(6)
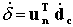 (7)
(7)
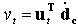 (8)
(8)
where, 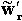 and
and 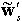 are angular velocities of
a roller and a segment with respect to each body reference frame, respectively.
The normal vector of
are angular velocities of
a roller and a segment with respect to each body reference frame, respectively.
The normal vector of 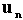 and tangent vector of
and tangent vector of 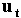 are determined as follows.
are determined as follows.
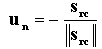 (9)
(9)
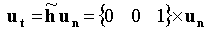 (10)
(10)
Finally, the contact normal force can be derived from Eqs. (2), (3) and (7) and the friction force are computed from Eqs. (5) and (8).
Roller and Roller Interactions
A roller to roller contact can be described as a circle-to-circle contact as shown in Figure 1.
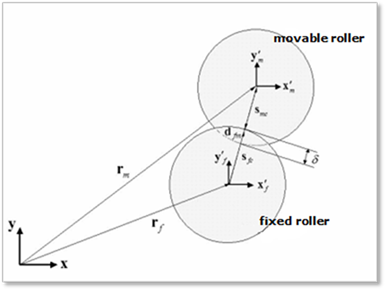
Figure 3 Roller and roller interactions
The relative displacement between a fixed roller and a movable roller can be computed with the following equation.
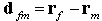 (1)
(1)
where, 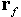 and
and 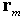 are the center
position vectors of the fixed roller and movable roller, respectively. The
vector of
are the center
position vectors of the fixed roller and movable roller, respectively. The
vector of 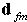 is projected by the body
reference frame of the fixed roller and the resultant vector can be represented
as follows.
is projected by the body
reference frame of the fixed roller and the resultant vector can be represented
as follows.
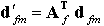 (2)
(2)
where, 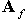 is the orientation matrix
of the fixed roller. From Eq. (2), the contacted penetration is determined as
follows.
is the orientation matrix
of the fixed roller. From Eq. (2), the contacted penetration is determined as
follows.
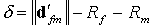 (3)
(3)
where, 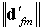 ,
, 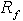 and
and 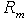 are the distance of
are the distance of 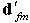 and the radii of the rollers,
respectively. The contact positions from the two roller centers can be computed
as follows.
and the radii of the rollers,
respectively. The contact positions from the two roller centers can be computed
as follows.
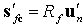 (4)
(4)
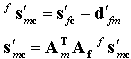 (5)
(5)
where, 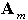 is the orientation matrix of the
movable roller.
is the orientation matrix of the
movable roller. 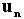 contains the normal direction
vectors and determined by following equation.
contains the normal direction
vectors and determined by following equation.
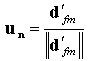 (6)
(6)
The positive normal direction is the same as the direction of the relative position vector between two roller center points. The tangent direction vector is determined by the right-hand rule. The relative velocity and the contact forces at the contact point can be computed similarly to the sheet and roller interactions.
Soft Nip and Maximum Gap of Movable Roller
The user can use a function expression of soft nip for adjusting the gap between two rollers. If the soft nip is activated, a dummy body that is connected to a base body by a translational joint is automatically created as shown in Figure 1. The translational direction of the dummy body for the soft nip is the same with the translation direction of the movable roller. The mass of the dummy body is zero and a motion of the translation joint is defined with the defined function expression. A roller axis retainer (RAR) to dummy contact is automatically created. The contact type is a circle to circle contact and the contact radii are determined with the same method used by Movable Roller and Fixed Roller.
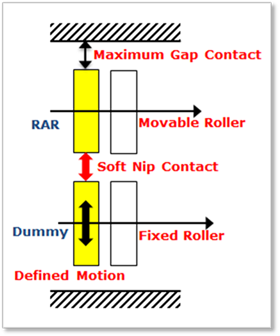
Figure 4 Soft nip and Maximum gap
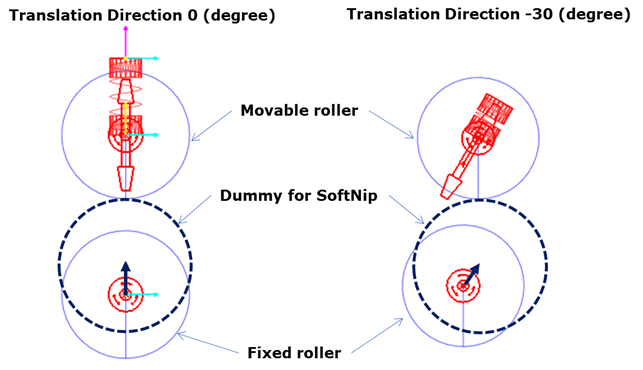
Figure 5 Soft nip
If a maximum gap is specified, a stopper activates when the Movable roller displacement reaches the designated value. In this case, RAR to base body contact is automatically created and its contact type is a point to circle contact. The contact radius and the point are determined by the radius of movable roller and the value of maximum gap, respectively.