Interpretation of Monte-Carlo Simulation Results

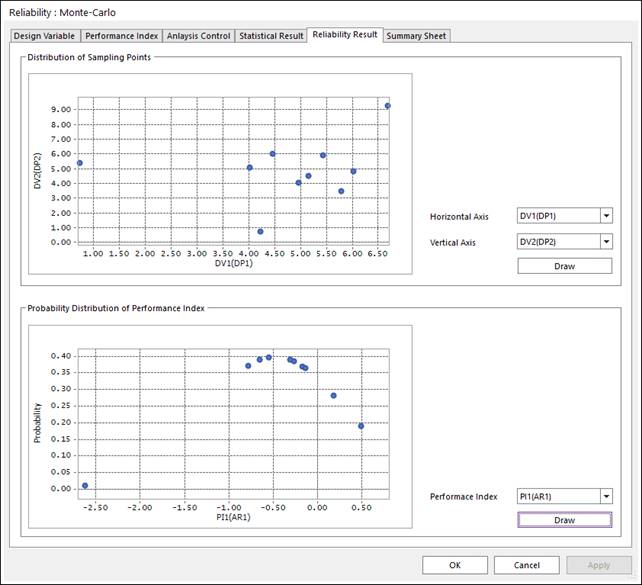
We provide two result sheets such as ‘Result Sheet’ and ‘Summary Sheet’. Figure 1 shows ‘Result Sheet’. In this sheet, you can see the sampling points and the probability distribution of performance index. When you see the sample points, first select two design parameters and push ‘Draw’ button. Then, you can see scattered points. Similarly, you can see the probability of the limit state function values (Performance Index values). In the probability distribution, minus (-) valued performance index (horizontal axis) denote failure zone.

Figure 1  Result Sheet of Monte-Carlo simulation

Although two constraint types are provided such as ‘Greater Than’ and ‘Less Than’, the internal solver use ‘Greater Than’ type constraint as a standard form. Thus, ‘Less Than’ type constraints are internally transformed into ‘Greater Than’ type constraints. Also, they are normalized by using their limit values.

Internal Conversion of Performance Index:

 for GE type

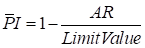 for LE type

As the constraint is ‘.LE.’ type in this problem, the internal performance index is transformed as

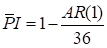
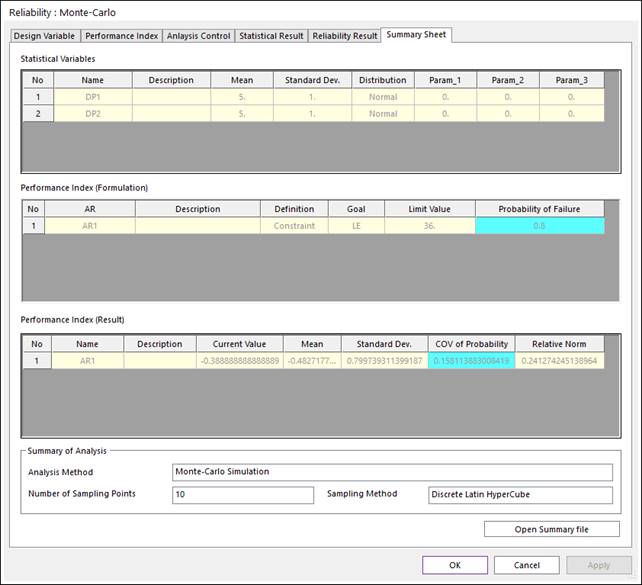
Figure 2  Summary Sheet of Monte-Carlo simulation

Figure 2 shows the summary sheet. In this sheet, the statistical information for random variables is listed. The values of Param_1 ~ Param_3 are parameters that represent the probabilistic distribution, which are internally calculated. Table 1 lists those parameters. The detailed information of those parameters is explained in Probability Distributions.

Table 1  Statistical Parameters for probabilistic distribution

The goal of Monte-Carlo simulation, failure property is listed in Performance Index (Formulation). In this problem, the failure of probability is obtained as 0.8 (80%).

In Performance Index (Result), ‘Current Value’ is PI value for the given mean values. ‘Mean’ and ‘Standard Dev’ are sample mean and sample standard deviation for PI values evaluated at sampled points. ‘COV of Probability’ is an important measure of Monte-Carlo simulation validation, which are evaluated as

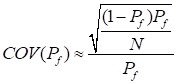
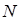The value of  is failure probability,  is number of sampled points. Smaller value of COV represents that the Monte-Carlo simulation gives more accurate result. ‘Relative Norm’ represents the normalized difference between ‘Current Value’ and ‘Mean’. Next, we will compare the accuracy of Monte-Carlo simulation by increasing the number of sample points.

Let’s consider the following ‘Adaptive Monte-Carlo Simulation’ concept. For more accurate estimation, we will use 20 sample points (new 10 points + 10 points get from simulation history). To do this, check ‘New Sampling’ and enter 10 in the column ‘Number of Sampling points’. Next, check ‘Get From Simulation History’ and get the 10 analysis results

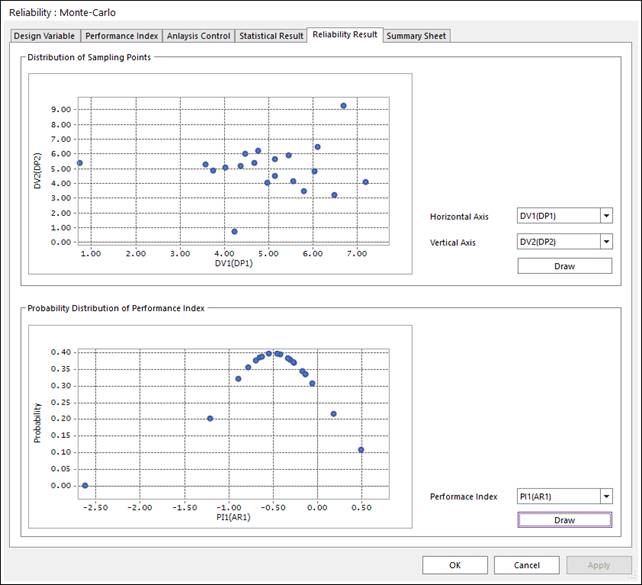
(a) Result Sheet for 20 sample points

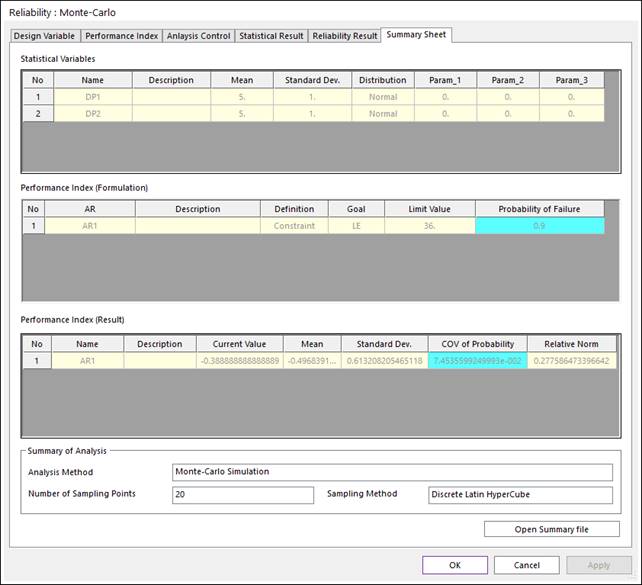
(b) Summary Sheet for 20 sample points

Figure 3  Analysis Results from 20 sample points

Figure 3 shows the analysis results for 20 sample points, respectively. Two figures show that failure probabilities converge from 0.8 to 0.9. Also, the COV values are sequentially reduced from 10 sample points (shown in Figure 2) to 20 sample points (shown in Figure 3).