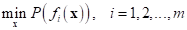
Multi-objective optimization strategy gives non-unique solution. Let’s consider the typical optimization formulation as
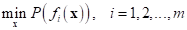
Where, the design variable vector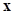 
belong to the feasible set 
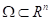, defined by equality and
inequality constraints as
.
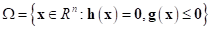Also,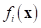 
is the ith
objective and the functional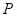 
is called as a preference function.
Unlike a single objective, multi-objective optimization has
no unique solution that would give an optimum for all objectives simultaneously.
We call it as a Pareto optimal. A solution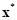 
is Pareto optimal if there exists no
feasible point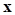 
which
would decrease some objectives without causing a simultaneously increase in at
least one objective. Figure 1 shows the Pareto optimum.
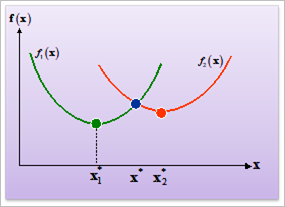
Figure 1 Local Pareto optimum in two objective case
Two points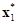 
and 
are local optima for objectives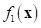 
and 
, respectively. In multi-objective
optimization, they are called as an ideal optimum and the point 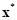is a local Pareto optimum.