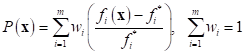
In general, numerical optimization, multi-objective is transformed into a single functional called as a preference function. There are several types of preference function such as weighed summation type, weighted distance type and weighted min-max type.
•Weighted Summation Type
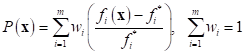
•Weighted Distance Type

•Min-Max Type

Conceptually, each local optimum  is preferred as a
is preferred as a 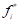 in the above formulations. In
practical design, no one knows them until solving each single objective
optimization. One guesses them properly or replaces them as
in the above formulations. In
practical design, no one knows them until solving each single objective
optimization. One guesses them properly or replaces them as  , where
, where 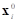 is the initial design point.
is the initial design point.
Now, we compare the optimization results for multi-objective
formulations. Suppose that 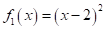 and
and 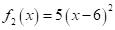 will be minimized simultaneously.
Figure 1 shows them.
will be minimized simultaneously.
Figure 1 shows them.
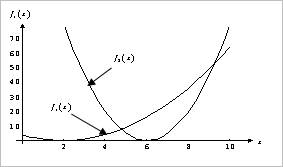
Figure 1 Graphical representation of two objectives
If the same weightings are used in these two objectives,
Figure 1 shows that the pareto optimum is  and
and 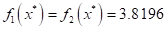 .
.
•Weighted Summation Type
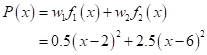
As the optimum satisfies 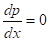 , it gives
, it gives
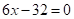
Thus, the optimum is 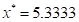 , which is different from the Pareto
optimum.
, which is different from the Pareto
optimum.
•Weighted Distance Type
Let the value of 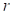 be 2. Then, the distance function
is
be 2. Then, the distance function
is
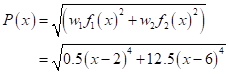
By solving 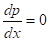 ,
,

This gives that 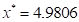 , which is different from the Pareto
optimum.
, which is different from the Pareto
optimum.
•Weighted Min-Max Type
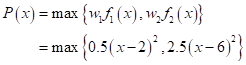
This functional is a composite non-smooth function as follows:
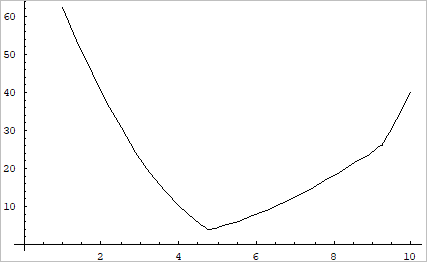
Figure shows that this formulation gives the Pareto optimum
 but it requires some special
techniques to overcome the non-smoothness of functional. This is the reason that
the min-max type is not used in the gradient-based optimization, even though it
can guarantee a local Pareto optimum.
but it requires some special
techniques to overcome the non-smoothness of functional. This is the reason that
the min-max type is not used in the gradient-based optimization, even though it
can guarantee a local Pareto optimum.