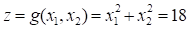
Let’s reconsider the example problem explained in the Example for Normal Distributions of Monte Carlo Simulation. The performance function of a mechanical system is given by
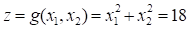
Where  and
and
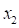 are the random
variables with normal distributions. Their mean values and standard deviation
values are (10,10) and (5,5), respectively. If the performance function
are the random
variables with normal distributions. Their mean values and standard deviation
values are (10,10) and (5,5), respectively. If the performance function 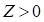 , then the system is always safe.
Find the probability of failure for the mechanical system.
, then the system is always safe.
Find the probability of failure for the mechanical system.
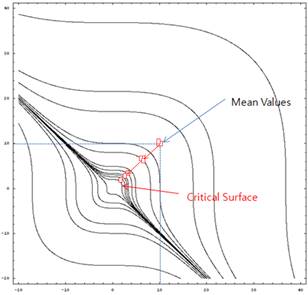
Figure 1 The convergence trajectory by AFORM in AutoReliability
Sol: Numerical optimization approach of AutoReliability provides three methods such as ‘AFORM’, ‘AFORM+DRM1’, and ‘AFORM+DRM2’. All methods are based on Meta-model based SAO, which uses similar concept of AutoDesign. The sequence, however, is more efficient than that of AutoDesign because the design problem for reliability analysis is only one formulation unlike the general optimization.
Figure 1 shows the convergence trajectory of AFORM (Advanced First-Order Reliability Method) which solve the reliability index analysis problem by using meta-model based SAO. It requires only 17 evaluations until converged. Among them, 13 evaluations, sampled from discrete Latin Hypercube design, are used to construct the initial meta-model. The remaining 4 points are used to validate the results obtained in the SAO steps. The most probable failure point is (1.9897, 2.1632). The probability of failure is 0.01250 and the reliability index is 2.2412.
Next, AFORM+DRM-1 employs the MPFP based DRM. This method employs the numerical integration for the meta-model at MPFP. Thus, it does not require additional evaluation than AFORM. Thus, it requires only 10 evaluations. The estimated failure probability and the reliability index are 0.006689 and 2.4745, respectively.
Finally, Figure 2 shows the convergence trajectory by AFORM+DRM2. Unlike AFORM+DRM-1, this method samples the exact evaluations when the numerical integration at MPFP. The 5-point gauss integration is used. Thus, it requires the additional evaluations such as 4*(NDV-1) points. Thus, it requires 14 points (10 evaluations for AFORM and 4 evaluations for integration). The estimated failure probability and the reliability index are 0.00666 and 2.4745, respectively. These values are exactly equal to that of AFORM+DRM1, which represents the meta-model is nearly exact about MPFP.

Figure 2 The convergence trajectory by AFORM+DRM2 in AutoReliability
Comparing with the results of Monte-Carlo simulation
shown in the figure,
the probability of failure (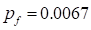 )
of the SAO based approach is nearly equal to that of Monte-Carlo 5000
simulations (
)
of the SAO based approach is nearly equal to that of Monte-Carlo 5000
simulations (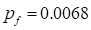 ). However, it
is noted that AFORM+DRM1 and AFORM+DRM2 used only 17 and 21
evaluations, respectively.
). However, it
is noted that AFORM+DRM1 and AFORM+DRM2 used only 17 and 21
evaluations, respectively.