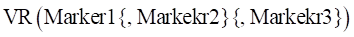
The VR function returns the change in two markers’ relative velocity and/or breakaway direction. A positive value (+) indicates that the distance between the two markers is growing. A negative value (-) value indicates that the distance between the two markers is shrinking.
Format
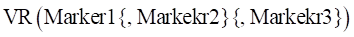
Arguments definition
|
Marker1 |
The name or argument number of a marker to be calculated |
|
Marker2 |
The name or argument number of a marker to be calculated •If omitted, then the InertiaMarker is applied. |
|
Marker3 |
The name or argument number of the reference marker that will serve as the standard marker for the velocity vector •Marker3 must be the same value as Marker2. If omitted, then the InertiaMarker is applied. |
Formulation
:
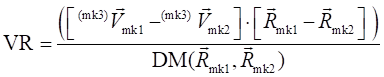
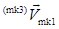Marker1's velocity vector from Marker3
:
Marker2's velocity vector from Marker3
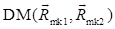: Distance
from the 
vector to the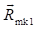 
vector
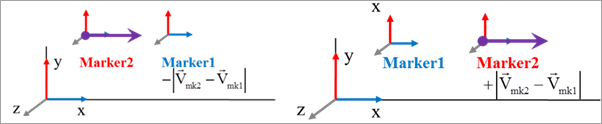
<approaching> <breakaway>
Example
VR (body1.marker1)
VR (body1.marker1, body2.marker2)
VR (body1.marker1, body2.marker2, body2.marker2)
VR (1,2,2) <Argument: (1)body1.marker1, (2)body2.marker2>
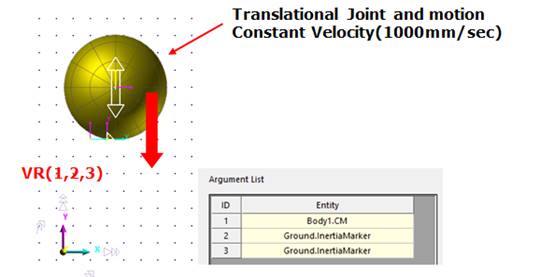
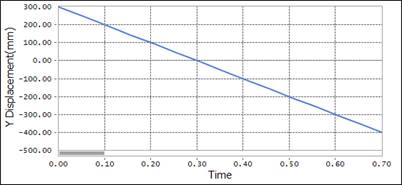
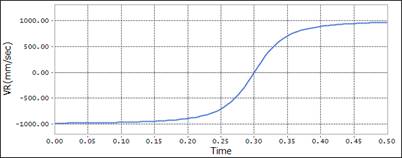
As shown in the following figure, Body1 is placed at (50,300,0) and a translational joint is modeled. This joint is assigned a motion velocity of 1000 mm/sec. By applying the VR function for the InertiaMarker and CM marker to InertiaMarker and Body1, the displacement in the y direction and the VR function results are retrieved, as shown in the following graphs. One of the key examples of a real life application of the VR function is an expression-used to model dampers (shock Absorbers) on automobile suspension systems.
