RecurDyn offers two solutions of an undamped system and a damped system.

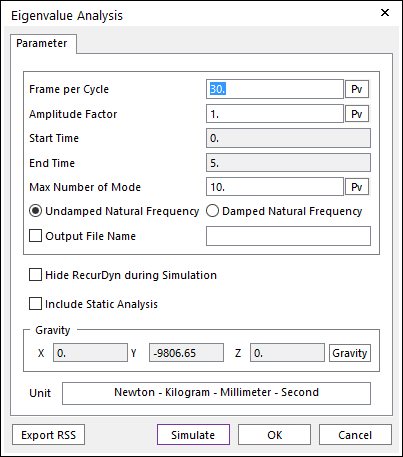
Figure 1 Eigenvalue analysis dialog box
Undamped System
Undamped system focuses on the result of undamped
natural frequency. To get the solution, RecurDyn solver ignores the
damping matrix (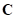 ) of
the system. Therefore, Eigensolver computes with Eq.(15) in spite of
using Eq (2).
) of
the system. Therefore, Eigensolver computes with Eq.(15) in spite of
using Eq (2).
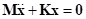 ,
, 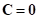 (15)
(15)
In undamped system, the damping is ignored. Always the real
(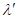 ) of eigenvalue is computed in
undamped system. The undamped natural frequency (
) of eigenvalue is computed in
undamped system. The undamped natural frequency (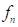 ) as follows :
) as follows :
 [Hz]
(16-1)
[Hz]
(16-1)
If the computed the real eigenvalue (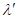 ) is positive value then the mode
doesn’t have an undamped natural frequency. At this time the reported value is
defined as follows :
) is positive value then the mode
doesn’t have an undamped natural frequency. At this time the reported value is
defined as follows :
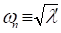 [rad/time]
(16-2)
[rad/time]
(16-2)
Also, in the 1-DOF undamped system, we can define the undamped natural frequency from the analytic solution as follows:
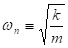 (17)
(17)
To get the solution of an undamped system, choose the undamped natural frequency on the analysis dialog as shown in Figure 1
Damped System
Damped system includes the damping of the
system. From the result Eq. (14), we call the 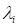 as the damped natural frequency (
as the damped natural frequency (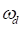 ) as follows:
) as follows:
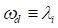 (18)
(18)
And also, in the 1-DOF damped system, we can define
the damping ratio (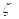 ) and
critical damping coefficient (
) and
critical damping coefficient (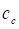 )as follows:
)as follows:
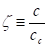 (19)
(19)
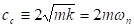 (20)
(20)
Here, the 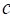 is the damping coefficient. Also, in
the damped system, if the damping coefficient is less than the critical damping
coefficient (
is the damping coefficient. Also, in
the damped system, if the damping coefficient is less than the critical damping
coefficient (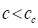 ) then, we can
also calculate the undamped natural frequency (
) then, we can
also calculate the undamped natural frequency (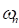 ) and damping ratio (
) and damping ratio (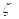 ) as follows:
) as follows:
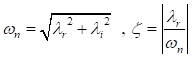 (21)
(21)
To get the solution of the damped system, choose the damped natural frequency on the analysis dialog as shown in Figure 1.
NOTE
When imaginary value of an eigen value is close to zero, the undamped natural frequency cann’t be defined like as Eq (21). In that time the undamped natural frequency will be set zero value.
Additional Information on Undamped System
Generally, the eigenvalue(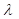 ) can be obtained as
follows.
) can be obtained as
follows.
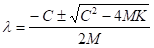 (22)
(22)
where 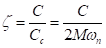 ,
, 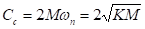
Hence, the general solution is given by following equation as shown Eq. (23) below.
 (23)
(23)
where 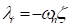 ,
, 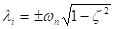
At this point, in case of the undamped system which has the
real eigenvalue(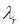 ) as zero, the eigenvalue
should be came from just the imaginary eigenvalue(
) as zero, the eigenvalue
should be came from just the imaginary eigenvalue(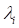 ). So, because the imaginary
eigenvalue(
). So, because the imaginary
eigenvalue(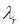 ) has two roots which are
conjugate complex value, if the imaginary eigenvalue(
) has two roots which are
conjugate complex value, if the imaginary eigenvalue(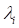 ) is zero, the solver should
show two eigenvalue as zero.
) is zero, the solver should
show two eigenvalue as zero.