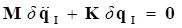Undamped system

To obtain Eigenvalue we reorganize matrices from linearization as Eq. (1). Damping matrix is ignored in this analysis option.

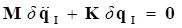                            (1)

Where,and 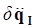 are displacement, acceleration of the independent coordinate, respectively. 

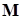 and 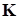 are the mass matrix, stiffness matrix, respectively.

The equation of motion can be expressed as follows:

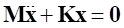                                       (2)

Where, 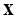 is independent coordinates.

In order to solve the Eq. (2), let’s assume the solution as follows:

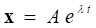
Therefore, if we substitute 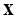 to the equation of motion,

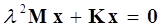                                          (7)

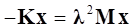                                                (8)

If we multiply the inverse of modified mass matrix (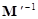) to Eq. (4), then

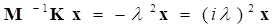                                                   (9)

If we define the 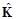 as follows,

                                                    (10)

Then,

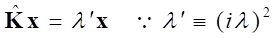                                                   (11)

If we consider the standard form of Eigenvalue problem as follows:

                                                    (12)

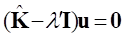                                                  (13)

In Eq. (12), the standard form of Eigenvalue problem is exactly same with our equation form of Eq. (11). Therefore we can get the Eigenvalue () and Eigenvector () from the Eigensolver. Here, the real Eigienvalue () of the undamped system can be recalculated as follows:

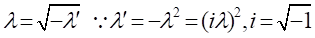                                 (14)