 is defined over the range
is defined over the range  and approaches one as
and approaches one as  according to the relation.
according to the relation.
Maximum Value Distribution
The type-II asymptotic distribution for the maximum
values is useful whenever the parent distribution  is defined over the range
is defined over the range  and approaches one as
and approaches one as  according to the relation.
according to the relation.

where, 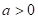 and
and 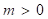 are the parameters of the
distribution. The extreme value distribution for the maximum value,
are the parameters of the
distribution. The extreme value distribution for the maximum value, 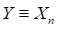 , is given by
, is given by
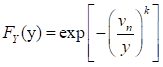
The corresponding PDF is

where 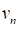 and
and
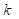 are the parameters of
the distribution;
are the parameters of
the distribution; 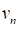 is
the characteristic maximum value of the underlying variable
is
the characteristic maximum value of the underlying variable 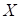 and
and 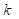 , the shape parameter, is a measure of
dispersion. The Type-II asymptotic form is obtained as
, the shape parameter, is a measure of
dispersion. The Type-II asymptotic form is obtained as 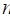 goes to infinity from an initial
distribution that has a polynomial tail in the direction of the extreme value,
which requires a polynomial tail. Therefore, a lognormal distribution converges
to a Type-II asymptotic form for the maximum value. However, the
Type-I converges from an exponential tail.
goes to infinity from an initial
distribution that has a polynomial tail in the direction of the extreme value,
which requires a polynomial tail. Therefore, a lognormal distribution converges
to a Type-II asymptotic form for the maximum value. However, the
Type-I converges from an exponential tail.
For the Type-II distribution of maxima, the mean,
standard deviation, and COV of 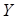 are related to the distribution
parameter
are related to the distribution
parameter 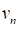 and
and 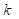 as follows:
as follows:
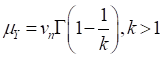
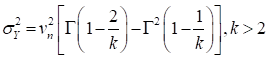
and
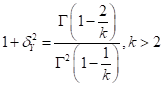
In these equations, 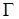 is the gamma function. It is useful
for representing annual maximum winds and other meteorological and hydrological
phenomena.
is the gamma function. It is useful
for representing annual maximum winds and other meteorological and hydrological
phenomena.
Minimum Value Distribution
The Type-II asymptotic distribution for the minimum
values is useful whenever the parent distribution  is defined over the range
is defined over the range 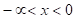 . In this case, the distribution
function for the minimum value,
. In this case, the distribution
function for the minimum value, 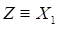 , is given by
, is given by
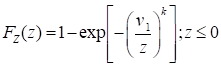
where the parameter 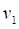 is the characteristic minimum value
of the initial variable
is the characteristic minimum value
of the initial variable 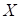 and
and 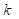 is the shape parameter, an inverse
measure of dispersion.
is the shape parameter, an inverse
measure of dispersion.
For the Type-II distribution of minima, the mean,
standard deviation, and COV of 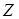 are related to the distribution
parameter
are related to the distribution
parameter 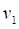 and
and 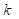 as follows:
as follows:

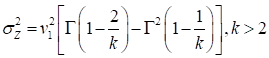
and
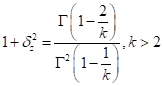
In these equations, 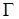 is the gamma function. It is not
commonly used since the required parent distribution shape is not commonly
observed in practical applications.
is the gamma function. It is not
commonly used since the required parent distribution shape is not commonly
observed in practical applications.