 is not bounded, which is of
an exponential type. In such a case, the distribution function can be expressed
as
is not bounded, which is of
an exponential type. In such a case, the distribution function can be expressed
as
Maximum Value Distribution
This distribution is, referred to as the Gumbel
distribution, useful when the right tail of the parent distribution  is not bounded, which is of
an exponential type. In such a case, the distribution function can be expressed
as
is not bounded, which is of
an exponential type. In such a case, the distribution function can be expressed
as

where 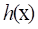 increases with x monotonically. The
distributions such as normal, log-normal and gamma distributions belong to this
category. The extreme value distribution for the maximum value,
increases with x monotonically. The
distributions such as normal, log-normal and gamma distributions belong to this
category. The extreme value distribution for the maximum value, 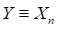 , is given by
, is given by
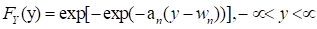
where the parameters of distribution, 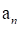 and
and 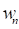 , can be determined from the observation
data. They are related to the mean and the standard deviation of the extreme
value
, can be determined from the observation
data. They are related to the mean and the standard deviation of the extreme
value 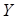 as
as
 and
and

Where 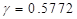 is the Euler’s constant.
is the Euler’s constant.
Minimum Value Distribution
This distribution is useful whenever the left tail of the
parent distribution is unbounded and decreases to zero towards the left in an
exponential form. In this case, the distribution function for the minimum value,
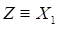 , is given by
, is given by
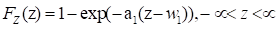
where, 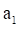 and
and 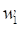 are the parameters of the
distribution. They are related to the mean and the standard deviation of the
extreme value
are the parameters of the
distribution. They are related to the mean and the standard deviation of the
extreme value 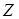 as
as
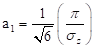 and
and
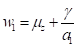
Where 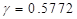 is the Euler’s constant.
is the Euler’s constant.