The user can use a general constraint as follows:
Spherical Joint
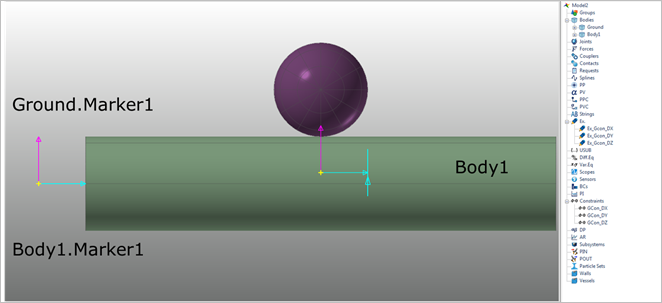
1. To make the spherical joint, create the any body.
2. Create a marker in the ground.
3. Create a marker in the body at the same position of a marker of ground.

Figure 1 Create body and marker
4. Make three general constraint expression for constraint 3 translation DOF.
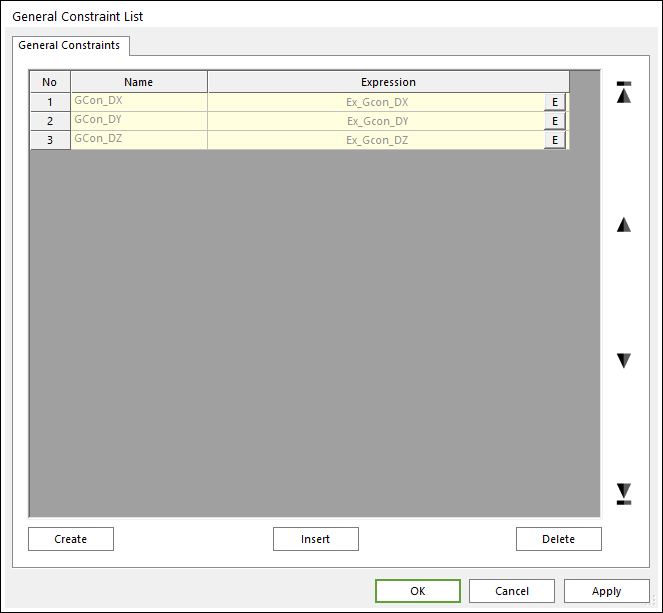
Figure 2 General Constraint List dialog box
5. Gcon_DX, Gcon_DY, Gcon_DZ mean distances of Ground.Marker1 and Body1.Marker1 each axis of Body1.Marker1 are ZERO.
•General Constraint Expression.
•DX(Ground.Marker1,Body1.Marker1) = ZERO
•DY(Ground.Marker1,Body1.Marker1) = ZERO
•DZ(Ground.Marker1,Body1.Marker1) = ZERO
Distance Joint
1. To make the distance joint, create the any body.
2. Create a marker in the ground.
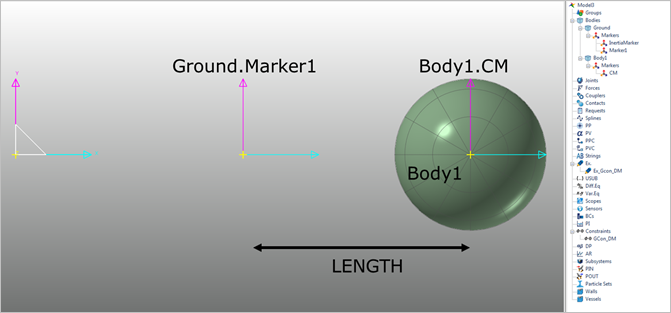
Figure 3 Create body and marker
3. Make a general constraint expression for constraint same distance.
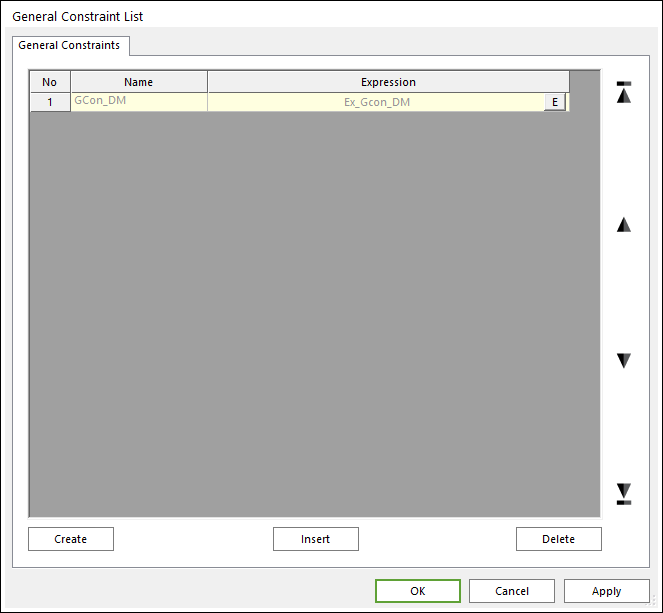
Figure 4 General Constraint List dialog box
4. Gcon_DM mean distances of Body1.CM and Ground.Marker1 each axis of Ground.Marker1 minus LENGTH are ZERO.
•General Constraint Expression.
•DM(Body1.CM,Ground.Marker1) – LENGTH = ZERO
CAUTION
•The LENGTH is not be ZERO in using DM expression.
•DM(1,2) = ZERO is not define the direction of reaction force. So the simuation will be stopped.
Revolute Joint
1. To make the revolute joint, create the any body.
2. Create two markers in the ground for the vector equation.
•These two markers represent the Z vector of base body.
3. Create three markers in the body for the vector equation.
•These three markers represent each X and Y vector of action body.
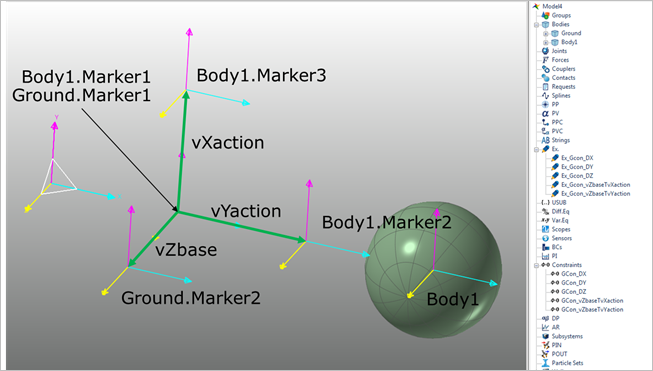
Figure 5 Create body and marker
4. Make five general constraint expression for constraint 3 translation and 2 rotation DOF.
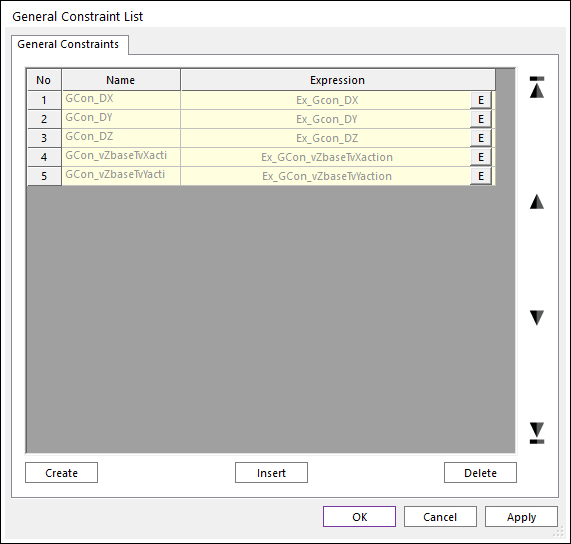
Figure 6 General Constraint List
5. These general constraint equations mean base marker and action marker are same position and only Z vector direction of base is free.
•General Constraint Expression.
•DX(Body1.Marker1,Ground.Marker1) = ZERO
•DY(Body1.Marker1,Ground.Marker1) = ZERO
•DZ(Body1.Marker1,Ground.Marker1) = ZERO
•DX(Ground.Marker2,Ground.Marker1)*DX(Body1.Marker2,Body1.Marker1) + DY(Ground.Marker2,Ground.Marker1)*DY(Body1.Marker2,Body1.Marker1) + DZ(Ground.Marker2,Ground.Marker1)*DZ(Body1.Marker2,Body1.Marker1) = ZERO
•DX(Ground.Marker2,Ground.Marker1)*DX(Body1.Marker3,Body1.Marker1) + DY(Ground.Marker2,Ground.Marker1)*DY(Body1.Marker3,Body1.Marker1) + DZ(Ground.Marker2,Ground.Marker1)*DZ(Body1.Marker3,Body1.Marker1) = ZERO
Wire System
Wire System can be modeled mathematically by using General Constraint. An example model is provided in RecurDyn (<Install Dir>\Help\Examples\General Constraint).
About the example model, the wire is stretched to 100 mm for 1 second and then third pulley moves 50 mm for 2 seconds.
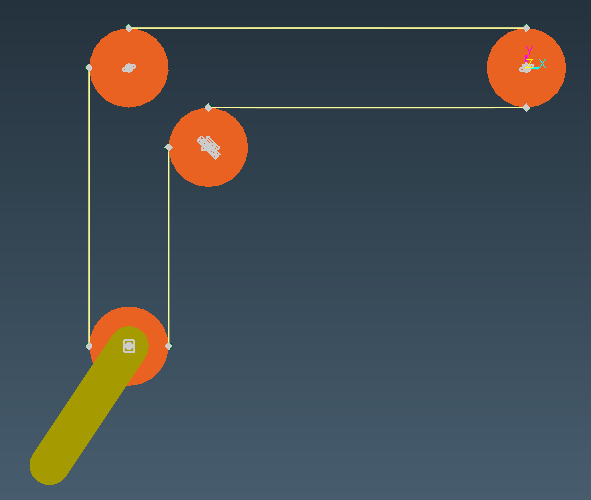
Figure 7 Example model
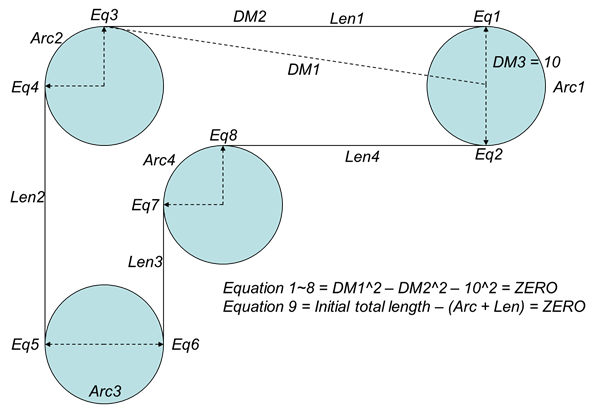
Figure 8 Mathematical equations of the example model