Three-Level Orthogonal Design
Three-Level orthogonal design is a fractional
factorial of  . For
. For 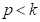 , the
, the 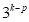 fractional design first generates
fractional design first generates
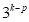 full factorials for
full factorials for
 factors. Then, the
remaining
factors. Then, the
remaining 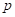 columns are
determined from the pre-generated
columns are
determined from the pre-generated  columns. To do these, a defining relation
is introduced as
columns. To do these, a defining relation
is introduced as 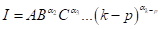 . The
component of the
. The
component of the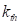 column is
determined as
column is
determined as
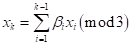 where,
where, 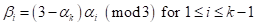 .
.
As an example, we generate 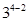 fractional factorial design with
fractional factorial design with  and
and 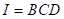 . From the rules, the 3rd and 4th columns
are
. From the rules, the 3rd and 4th columns
are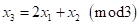 and
and  . These results are listed side by side in
Table 1.
. These results are listed side by side in
Table 1.

Table 1 A fractional factorials of 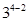 with
with  and
and 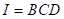
The above factorial design of 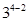 is only one of the
is only one of the 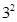 fractions of
fractions of 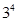 full factorial designs. Among those
full factorial designs. Among those
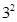 fractions, only the
cases that are orthogonal between columns are the three-level orthogonal array
for
fractions, only the
cases that are orthogonal between columns are the three-level orthogonal array
for  . Hence, the
defining relation for
. Hence, the
defining relation for 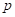 factors
is very important to maintain the orthogonal characteristics in the columns.
factors
is very important to maintain the orthogonal characteristics in the columns.
We support the automatic generator for the three-level
orthogonal array design. If one define the number of factors  , the
RecurDyn/AutoDesign automatically generates the
, the
RecurDyn/AutoDesign automatically generates the 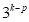 fractional factorials, where
fractional factorials, where
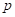 is internally
determined as possible as minimize the trials.
is internally
determined as possible as minimize the trials.

Reference
1. Peter W.M. John, 1998,
Statistical Design and Analysis of Experiments, SIAM, Philadelphia.
2. Douglas C Montgomery, 2000,
Design and Analysis of Experiments, John Wiley & Sons, New York.
 . For
. For 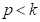 , the
, the 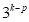 fractional design first generates
fractional design first generates
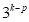 full factorials for
full factorials for
 factors. Then, the
remaining
factors. Then, the
remaining 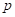 columns are
determined from the pre-generated
columns are
determined from the pre-generated  columns. To do these, a defining relation
is introduced as
columns. To do these, a defining relation
is introduced as 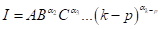 . The
component of the
. The
component of the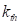 column is
determined as
column is
determined as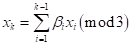 where,
where, 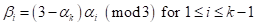 .
.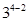 fractional factorial design with
fractional factorial design with  and
and 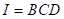 . From the rules, the 3rd and 4th columns
are
. From the rules, the 3rd and 4th columns
are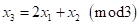 and
and  . These results are listed side by side in
Table 1.
. These results are listed side by side in
Table 1.
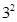 fractions of
fractions of 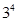 full factorial designs. Among those
full factorial designs. Among those
 . Hence, the
defining relation for
. Hence, the
defining relation for  , the
RecurDyn/AutoDesign automatically generates the
, the
RecurDyn/AutoDesign automatically generates the 