Small Composite Design (SCD)
Hartley (1959) pointed out that, for estimation of the
second-order surface, the cube portion of the central composite design (CCD)
need not be of resolution 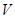 .
It could be of resolution as low as
.
It could be of resolution as low as  , provided that two-factor interactions
were not aliased with other two-factor interactions. Hartley employed a smaller
fraction of the
, provided that two-factor interactions
were not aliased with other two-factor interactions. Hartley employed a smaller
fraction of the  factorial than is used in the
original Box-Wilson designs and so reduced the total number of points. Hartley’s
cubes may be designated resolution
factorial than is used in the
original Box-Wilson designs and so reduced the total number of points. Hartley’s
cubes may be designated resolution  , meaning a design of resolution
, meaning a design of resolution  but with no words of length
four in the defining relation.
but with no words of length
four in the defining relation.
Westlake (1965) provided a method for generating composite
designs based on irregular fractions of the  factorial system rather than using
the complete factorials or regular fractions of factorials employed by Box and
Wilson (1951) and Hartley (1959). Westlake provided three examples for 22-run
designs for
factorial system rather than using
the complete factorials or regular fractions of factorials employed by Box and
Wilson (1951) and Hartley (1959). Westlake provided three examples for 22-run
designs for 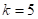 , one example of
a 40-run design for
, one example of
a 40-run design for 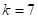 , and one
example of a 62-run design for
, and one
example of a 62-run design for 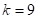 .
.
Draper (1985, 1990) proposed an alternative approach to
obtaining small composite design (SCD), which employed columns of the
Plackett-Burman designs (1946) rather than regular or irregular
fractions. Draper (1985) and Draper and Lin (1990) have shown that many small
composite designs exist. The formation of these designs is constructed by (1)
using the 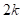 axial runs
plus center runs, (2) adding the
axial runs
plus center runs, (2) adding the 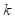 columns of a Plackett-Burman
design for the cube portion to avoid singularity or near singularity, (3)
while removing one of each set of duplicates if duplicate runs exist.
columns of a Plackett-Burman
design for the cube portion to avoid singularity or near singularity, (3)
while removing one of each set of duplicates if duplicate runs exist.
Draper provided, using 12-run, 28-run and 44-run
Plackett-Burman designs, 22-run design for 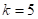 , 42-run design for
, 42-run design for 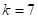 and 62-run design for
and 62-run design for 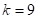 , respectively. However, his approach
cannot give a general design assessed on the number of factors, because it is
another optimization problem. For the detailed information, one may refer to the
references (Draper, 1985; Draper and Lin, 1990).
, respectively. However, his approach
cannot give a general design assessed on the number of factors, because it is
another optimization problem. For the detailed information, one may refer to the
references (Draper, 1985; Draper and Lin, 1990).
In AutoDesign, an automated version of SCD is
presented. This design gives slightly super-saturated samplings for the
second-order response surface model. We call it as a generalized small composite
design (GSCD).
For the large scaled second-order response surface model,
GSCD still requires many samplings, even though it can reduce the number
of sampling points than CCD and BBD. Hence, we develop new sub-saturated
sampling methods. We call them as incomplete small composite designs
(ISCD). They are divided into two methods. One is an incomplete small
composite design-I (ISCD-I). Another is an incomplete small composite
design-II (ISCD-II). The ISCD-I reduces the points in the cube
portion of GSCD. Then, the ISCD-II removes the star points of the
ISCD-I.
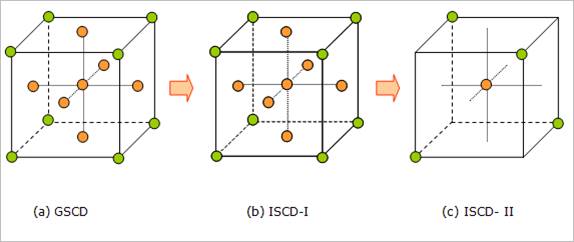
Figure 1 Geometric views of three small composite
designs
In Table 1, the total number of points in cube and star,
excluding center point, in various small composite designs previously discussed,
are summarized.
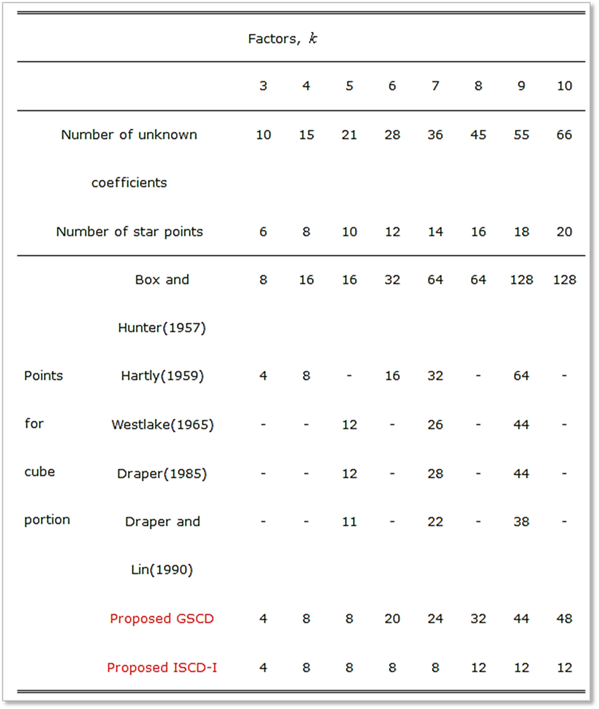
Table 1 Experimental points excluding center point in
some small composite designs
The symbol ‘-’ denotes that the design is not provided by the
authors.
Reference
1. Box, C.E.P. and Hunter, W.G.,
1957, “Multi-factor Experimental Designs for Exploring Response Surfaces”,
Annals of Mathematical Statistics, Vol. 28, pp. 195~241.
2. Hartly, H.O., 1959, “Small
Composite Design for Quadratic Response Surfaces”, Biometrics, Vol. 15,
pp.611~624.
3. Westlake,W.J., 1965, “Composite
Design based on Irregular Fractions of Factorials”, Biometrics, Vol. 21,
pp. 324~336.
4. Draper, N.R., 1985, “Small
Composite Designs”, Technometrics, Vol. 27, No. 2, pp. 173~180.
5. Draper, N.R. and Lin, D.K., 1990,
“Small Response Surface Design”, Technometrics, Vol. 32, No. 2, pp.
187~194.
6. Kim M.-S and Heo S.-J., 2003,
“Conservative Quadratic RSM combined with Incomplete Small Composite Design and
Conservative Least Squares Fitting”, KSME International Journal, Vol. 17,
No. 5, pp. 698~707.
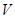 .
It could be of resolution as low as
.
It could be of resolution as low as  , provided that two-factor interactions
were not aliased with other two-factor interactions. Hartley employed a smaller
fraction of the
, provided that two-factor interactions
were not aliased with other two-factor interactions. Hartley employed a smaller
fraction of the  factorial than is used in the
original Box-Wilson designs and so reduced the total number of points. Hartley’s
cubes may be designated resolution
factorial than is used in the
original Box-Wilson designs and so reduced the total number of points. Hartley’s
cubes may be designated resolution  , meaning a design of resolution
, meaning a design of resolution  but with no words of length
four in the defining relation.
but with no words of length
four in the defining relation.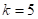 , one example of
a 40-run design for
, one example of
a 40-run design for 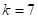 , and one
example of a 62-run design for
, and one
example of a 62-run design for 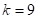 .
.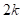 axial runs
plus center runs, (2) adding the
axial runs
plus center runs, (2) adding the 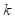 columns of a Plackett-Burman
design for the cube portion to avoid singularity or near singularity, (3)
while removing one of each set of duplicates if duplicate runs exist.
columns of a Plackett-Burman
design for the cube portion to avoid singularity or near singularity, (3)
while removing one of each set of duplicates if duplicate runs exist. 
