,
(1)
Now, one tries to minimize the performance modified as:
Minimize ,
(1)
where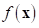 
and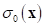 
are the performance and its variation
according to the design variable variation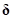 
. Also, the coefficients 
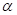and 
denotes the weighting factors for
them. In AutoDesign, 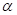and are called as the alpha weight and
the robust index for objective, respectively. If one tries to minimize only the
variance, he just set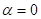 
and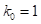 
.
AutoDesign uses the following 
during optimization process:
,
(2)
which is similar to Taylor series approximation for a
variance in statistics. If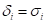 
for each design variable, then 
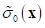will be the approximate
standard deviation of 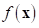directly. As one may not know 
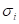in the practical design, he
or she will use the variation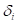 
simply. This represents that 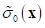can be a variation for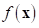, even though it is not the
approximation of standard deviation.
What is a robust design for constrained optimization problem?
Now, consider the robust design for it. First, let’s consider the equality
constraints. Suppose that an equality constraint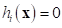 
is transformed into 
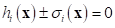as a robust design formulation. From the
definition of equality constraint, this transformed constraint is satisfied only
when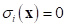
. It is unusual in the
practical design problem. Thus, one equality constraint can be divided into two
inequality constraints as:
,
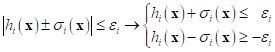(3)
where, 
is a limit value
defined by user. If a robust design formulation is required for equality
constraint, AutoDesign recommends that the user divide it into two
inequality constraints. Thus, when you define an equality constraint in the
window of Robust Design Optimization in AutoDesign,
Robust Index column will be deactivated automatically.
Second, let’s consider a robustness of inequality
constraints. AutoDesign has two types of inequality constraints such as
‘less than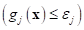
’ and ‘greater
than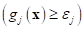
’ types. Their robust
formulations are represented as:
and
,
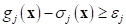(4)
where,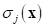 
can be evaluated similarly as (2).
Figure 1 shows the feasibility between a nominal optimum and a robust optimum.
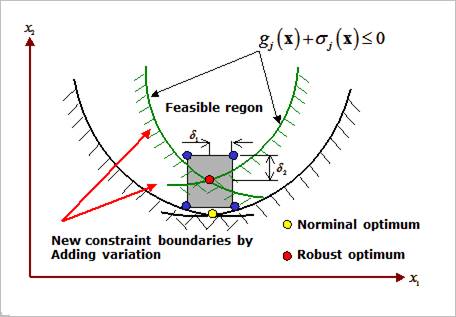
Figure 1 Robust design for inequality constraints
When the final design (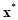
) has variations within 
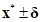, the final design is a robust optimum if
all the sampled responses 
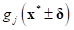are in the feasible region while
optimizing its’ objective.