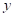depends on the controllable
input variables 
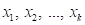. The
relationship i
Response surface Method is an integration of
statistical and mathematical techniques useful for developing, improving, and
optimizing process. The most extensive applications of RSM are in the
industrial world, particularly in situations where several variables potentially
influence some performance measure or quality characteristics of the product or
process. In general, a product or system response 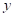depends on the controllable
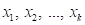input variables . The
relationship i
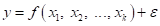
where the form of true response function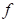 
is unknown and perhaps very
complicated, and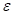 
is a
term that represents other sources of variability not included in 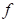. In general, the statistical error 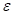is a normal distribution
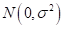. Suppose that the response
surface models 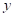may be
represented by
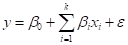(Linear Model) and
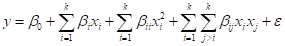(Quadratic Model)
Where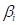 
are the unknown coefficients. If
there is more than one data point under consideration, the linear model is
extended to the matrix form
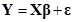
where 
is a
vector of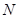 
observations, 
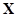is a matrix of known
constant,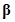 
is a vector
of 
parameters, and 
is the vector of random
errors. In order to obtain the unknown coefficients, we solve the sum of squares
of residuals as 
. To
minimize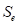
, we solve a set of
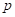equations. Hence the normal
equation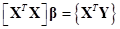 
is obtained.
The matrix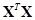 
is a symmetric
matrix with 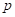rows and
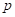columns. Its rank is the same
as the rank of 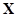, which is the
number of linearly independent column of .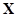
If the 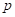columns of 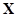are linearly independent, 
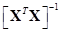exists and the normal
equations have a unique set of solutions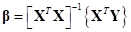
. However, if 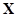is less than full rank because the
columns are not linearly independent,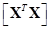 
is singular and 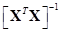does not exist. It will, in fact, be
true of almost the experimental design models. Hence special numerical
techniques are required to construct the general response surface modeling
tools.