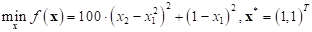
If ones construct the best meta-models, they use many sampling points in whole design space. Also, it is natural that best-meta models give good optimization results.
Suppose that the analysis time is much expensive, a negotiation is required for efficiency and best design. In general, optimization does not require the accurate meta-model through the design space. Although it starts with several points, SAO process finds new design points sequentially. These points are optimum candidates. Let’s consider the following case studies, which show their relations clearly.
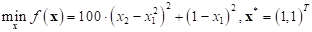
CASE 1: The initial sampling points are 200 from the discrete Latin hypercube method. The blue colored points are the initial sampling ones in Figure 1. Kriging method is employed for meta-model. AutoDesign requires 5 SAOs. Hence, it requires total 205 analyses. The red points are 5 SAO points in Figure 1.
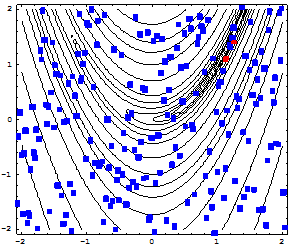
Figure 1 Case study 1: 200 sampling points
CASE 2: Now, only 20 sampling points are tried from the discrete Latin hypercube method. Then, Kriging model is used. In this case, AutoDesign requires 15 SAOs. Figure 2 shows the initial points (Blue) and the SAO ones (RED).
Figure 2 Case study 2: 20 sampling points
CASE 3: Finally, only 5 points are tried. These points came from Koshal Design. For fair comparison, Kriging meta-model is used. Then, AutoDesign requires 23 SAOs. Figure 3 shows the initial points (Blue) and SAO ones (RED).
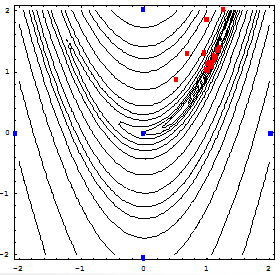
Figure 3 Case study 3: 5 sampling points
These case studies show that good sampling for optimization is not the number of sampled points but the well space filling of design space.
If one solves the deterministic optimization problem, ISCD-I sampling is recommended. If he wants to solve robust design or DFSS, Latin hypercube sampling is required.