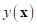to pass through all
sampling points using radial basis function 
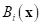and polynomial basis function
.
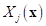Radial Basis Functions (RBF) are a class of functions
used for interpolation purposes. Their value depends on only on the distance
that is the radius between the generic point and center of the particular
function. The RBF method constructs the approximation function
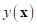to pass through all
sampling points using radial basis function 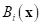and polynomial basis function.
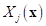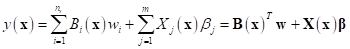
where,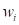 
is the weighting coefficient for 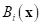and 
the coefficient for .
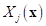A radial basis function has the following general form:
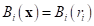
where,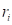 
is a distance between interpolating
point 
and the ith
sampled point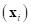 
. In general,
multiquadratics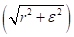 
and
Gaussian spline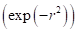 
is
widely used in the radial basis function.
In order to guarantee unique approximation, the following constraints are usually imposed to the polynomial term.
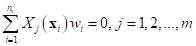
It is expressed in matrix form as follows:
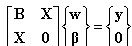
As the distance is scalar value, the 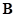matrix 
is symmetric. Hence the unique solution is
guaranteed if the inverse of matrix 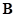exists.
Reference
1. Wang, J.G. and Liu, and G.R., “A point interpolation meshless method based on radial basis functions”, International Journal for Numerical Methods in Engineering, Vol. 54, pp. 1623-1648, 2002.
2. Jin, R., Chen, W. and Simpson, T.W., “Comparative studies of metamodeling techniques under multiple modeling criteria”, Struct. Multidisc. Optim., Vol. 23, pp. 1-13, 2001.