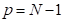 factors in
factors in 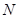 runs, where
runs, where 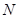 is a multiple of 4. If
is a multiple of 4. If 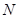 is a power of 2, these designs are
identical to those of
is a power of 2, these designs are
identical to those of 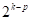 fraction factorial. However, for other
cases, the Plackett-Burman designs are sometimes of interest.
fraction factorial. However, for other
cases, the Plackett-Burman designs are sometimes of interest.
The original Plackett-Burman (1946) designs are
two-level fractional factorial designs for studying 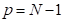 factors in
factors in 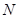 runs, where
runs, where 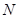 is a multiple of 4. If
is a multiple of 4. If 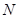 is a power of 2, these designs are
identical to those of
is a power of 2, these designs are
identical to those of 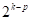 fraction factorial. However, for other
cases, the Plackett-Burman designs are sometimes of interest.
fraction factorial. However, for other
cases, the Plackett-Burman designs are sometimes of interest.
As an example, the Plackett-Burman design for  and
and 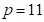 is derived. The element of
is derived. The element of 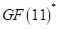 are 0, 1, 2, … , 10 with
arithmetic being carried out mod 11. The quadratic residues are
are 0, 1, 2, … , 10 with
arithmetic being carried out mod 11. The quadratic residues are 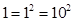 ,
, 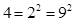 ,
, 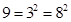 ,
, 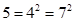 ,
, 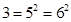 . Then
. Then 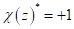 if
if  and
and 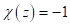 if
if 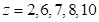 . These designs are shown in the following
table.
. These designs are shown in the following
table.

In AutoDesign, the Plackett-Burman design is extended
to overcome the lack of balance in some factors. As an example, the
Plackett-Burman design for 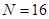 and
and 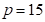 give imbalanced sampling, which is
only due to the quadratic residue of
give imbalanced sampling, which is
only due to the quadratic residue of 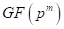 . In this case,
RecurDyn/AutoDesign automatically increase the number of
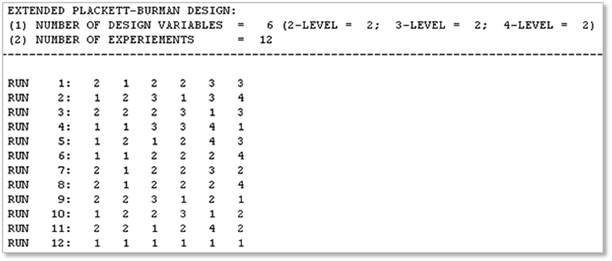
trials until satisfying the balance of sampling. Also, for the mixed-level
design such as 2, 3 and 4 levels, the contractive replacement method of Addelman
and Kempthorne (1961) is used. As an example, for the mixed-level such as two
2-level factors, two 3-level factors and two 4-level factors, the extended
Plackett-Burman design is given in the following table.
. In this case,
RecurDyn/AutoDesign automatically increase the number of
trials until satisfying the balance of sampling. Also, for the mixed-level
design such as 2, 3 and 4 levels, the contractive replacement method of Addelman
and Kempthorne (1961) is used. As an example, for the mixed-level such as two
2-level factors, two 3-level factors and two 4-level factors, the extended
Plackett-Burman design is given in the following table.
NOTE
Galois Field: Let z be any nonzero element of the finite
field 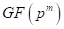 ;
;  is said to be a quadratic residue of
the field if there is an element
is said to be a quadratic residue of
the field if there is an element 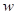 in the field such that
in the field such that 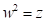 ; otherwise,
; otherwise,  is a nonquadratic residue. Then, the
Legendre symbol,
is a nonquadratic residue. Then, the
Legendre symbol, 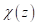 , is defined
as follows:
, is defined
as follows: 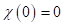 ;
; 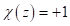 , if
, if  is a quadratic residue;
is a quadratic residue; 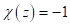 if
if  is a non-quadratic residue.
is a non-quadratic residue.
Reference
1. Plackett, R.L. and Burman, J.P., 1946, “The Design of Optimum Multi-factorial Experiments”, Biometrika, Vol. 33, pp. 305~325.
2. Addelman, S. and Kempthorne, O. 1961, “Some Main Effects Plans and Orthogonal Arrays of Strength Two”, Ann. Math. Statist., Vol. 32, pp. 1167~1176.
3. John, P.M.J., 1998, Statistical Design and Analysis of Experiments, SIAM, pp.185~190.