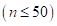 , this algorithm gives
very good performance.
, this algorithm gives
very good performance.
RecurDyn/AutoDesign provides the following three efficient design tools:
•Effect Analysis & Design Variable Screening
•Deterministic Optimization combined with Meta-Models
•Robust optimization & DFSS (Design for Six Sigma) combined with Meta-Models
In general, the design of experiments is classified with their application purposes. In other words, their sampling points are differently designed for the effect analysis and RSM. For the detailed information, refer to the theoretical background of DOE parts.
RecurDyn/AutoDesign provides the following DOE methods:
•DOE methods for Effect Analysis:
•Extended Plackett-Burman Design: It can generate a mixed level design (2-, 3-, and 4-levels) Absolutely, only 2-level DOE table can be generated.
•3-level Orthogonal Array Design: It can generate 3-level orthogonal array from 2 factors to 1000 factors.
•Level-Balanced Descriptive Design: It can generate the Strength-I orthogonal arrays for large-scaled design problem. Although its’ strength is worse than the strength-2 orthogonal array, it can be very effective DOE for large-scaled problem. As an example, if you want to generate only 200 sampling points for 20 factors with 10 levels, this method is adequate.
•Full Factorial Design: It is a classical DOE method, which is just only for small- scaled problem. We don’t recommend this DOE in the practical design.
•2-level Orthogonal Array Design: It can generate 2-level orthogonal array from 2 factors to 1023 factors.
•Bose’s orthogonal Array Design: It can generate an orthogonal table such as OA(q2,q+1,q,2), where q is a prime numbers (2, 3, 5, 7, 11, 13, 17 ….). In the notations OA(n, k, q, t) for an orthogonal array, the symbols ‘n’, ‘k’, ‘q’ and ‘t’ denote the number of runs, the number of available factors, levels and strength. Thus, Bose’s orthogonal array is a strength-2 orthogonal. Taguch’s L25(56) array employs Both’s OA(25,6,5,2).
•DOE methods for Meta-Modeling:
•Face Centered Central Composite Design: It is a classical DOE for quadratic RSM. It is not recommended in the practical design.
•Box and Behnken Design: It is a classical DOE for quadratic RSM. Although it can be efficient than CCD, we don’t recommend it for the practical design.
•Generalized Small Composite Design: In the late of 1980, Draper and his fellows developed to reduce the number of samplings in the classical CCD and SCD. We generalize their idea to generate DOE table automatically. Although GSCD is more efficient than CCD, it is not recommended in the large-scaled problem.
•Incomplete Small Composite Design-I and –II: These two methods reduce the number of sampling than GSCD. We recommended them for the large-scaled design problems.
•Discrete Latin Hypercube Design: As we explained, this is an efficient space filling method. Unlike the classical DOE, we can define the number of sampling points. As an example, if you want to 50 points for 20 factors, this method is adequate.
•Numerical Optimization Method:
•Augmented Lagrange Multiplier Method: It is well-known optimization algorithm. Especially, it gives best performance for large-scaled design problem.
•BFGS (quasi-Newton) method: For the small-scaled design
problem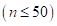 , this algorithm gives
very good performance.
, this algorithm gives
very good performance.
•Hestenes-Stiefel (conjugate Gradient) method: From the numerical
tests, conjugate gradient methods give more efficient results than quasi-Newton
method. In my empirical experience, conjugate gradient methods require only 23
gradient evaluations and 85 function evaluations to solve the large-scaled
problem 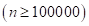 .
.
•Variable-order Polynomial Approximation method: This is an efficient one-dimensional search method, which uses average 3.5 function evaluations during line search process.
•Weighted Min-Max Formulation: There are many approaches to transform multiple objectives into an equivalent one such as weighting function, distance function and min-max function etc. Among them, only the min-max approach guarantees a unique solution.
•Meta-Modeling Techniques
•Simultaneous Kriging Method: Unlike the conventional DACE, the proposed method solves only the sub-optimization problem only one times, even though multiple responses are approximated. Hence, we call it as a simultaneous Kriging method. It is very accurate meta-modeling technique.
•Radial Basis Function Method: two RBF methods are supported such as Multi-qiadratics and Gaussian function. If the sampling points are more than 100, RBF with multi-quadratics is recommended.
•Conservative RSM: Unlike the conventional RSM, this method generates the over- and under-estimated RSM. This can be very effective in solving the optimization problem with noisy functions. However, we don’t recommend this method because the simultaneous Kriging can overcome the noisy results.
•Polynomial functions: All the three meta-modeling methods use the polynomial type regression models. Even though Bayesian method cannot uses polynomial type regression model, we combine them in order to reduce the sampling points. We provide 6 polynomial types such as constant, linear, diagonal quadratic, full quadratic, diagonal cubic and hybrid linear models. In RecurDyn/AutoDesign, these polynomial types are automatically switched during optimization process.
•[Extension] When the polynomial type is selected as ‘AUTO’, V7R1 internally switches the polynomial models into a diagonal quartic model to the degree of convergence.