Eigen Movement is a post-analysis toolkit. This function needs the eigenvalue analysis result especially the absolute eigenvector in the OUT file. If the absolute eigenvector is not in the OUT file, then this function doesn’t activate.
This function calculates the displacement vector from the initial to deformed position for a marker on the specific eigen mode.
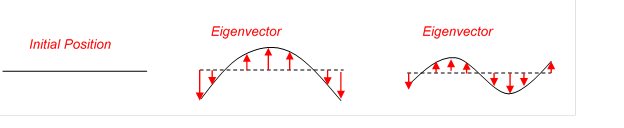
The physical meaning of the Eigenvector is a mode shape. Eigenvector is a displacement vector. Therefore, the eigen animation can be calculated that all bodies move from (InitialPos – Amplitude*Eigenvector) to (InitialPos + Amplitude*Eigenvector) during the animation frame.

Figure 1 Physical meaning of the eigenvector
The result is two displacement vectors both translation and rotation for moving with + absolute eigenvector. The rotation displacement vector is defined as a Bryant angle.
The calculation method:
•A marker of the Rigid body
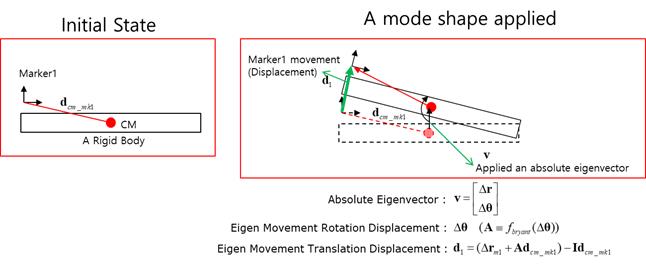
Figure 2 Algorithm for the Rigid body
•A marker of the RFlex body
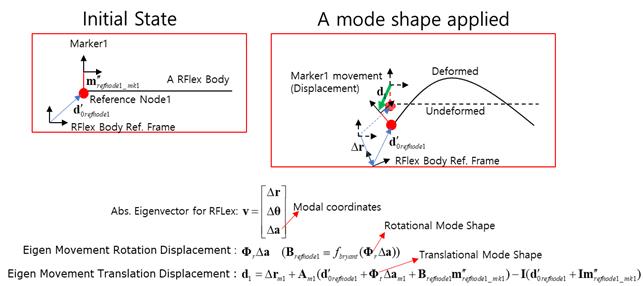
Figure 3 Algorithm for the RFlex body
Note
The Eigen Movement Vector uses absolute eigenvector defined as Cartesian coordinate. The Solver uses the relative coordinate. Therefore, the absolute eigen solver can be calculated using the Velocity Trasformation following equation.
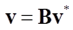
Where, v is the absolute eigenvector. B is the Velocity Transformation Matrix. v* is the eigenvector with relative coordinate.