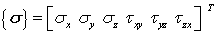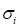are found by differentiating with
respect to the principle stretches, 
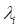
Hyperelastic
When the constitutive relationship is expressed in terms of
the strain energy density function, WD, the stress-stretch behavior is
found by differentiation with respect to the stretch. For the case of purely
incompressibility, the principle Cauchy stresses, 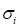are found by differentiating with
respect to the principle stretches,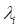
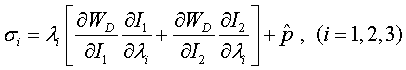
Where,
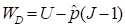: Energy density function
: Strain energy of each material type
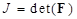: Volume change
: Displacement gradient
: Lagrange multipler
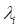: Principle stretches
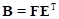: Left Cauchy-Green displacement tensor
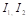: Invariant of B
:
:
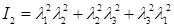Cauchy stress tensor is expressed with principle Cauchy stress tensor and orientation matrix.
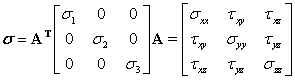
The stress components can also be expressed in vector for
