As you know, the numerical optimization algorithm requires many evaluations until converged. Thus, most of efficient optimization algorithm uses sequential approximation concepts such as Taylor series. They surrogate the exact responses with linear or quadratic functions. Then, sequentially solve the optimization problem composed of those approximate functions. These methods have been developed for structural optimization area based on linear static and normal model analysis, because the design sensitivity analysis (DSA) techniques were efficiently developed.
However, those design sensitivity analysis techniques is not developed for the multi-body dynamics, nonlinear FEA, and multi-physics solvers. Thus, the conventional optimization techniques cannot be used because Finite Difference Method based DSA requires too many evaluations. Also, function value based algorithms such as Genetic Algorithm and Simulated Annealing etc. do not uses directly because they require much more evaluations.
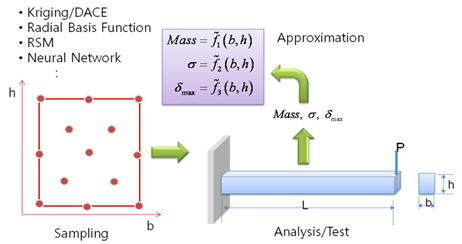
Thus, meta-model techniques introduced to make the approximate models in those areas. Then, the optimization algorithm can solve the design problem composed of approximate models. Meta-model is a generic name for approximate models. Figure 1 shows the general procedure for constructing meta-models.

Figure 1 Approximate modeling with meta-models