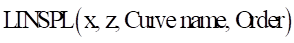
The LINSPL function uses Linear spline interpolation to return the y values for the x variable input through the spline entity.
Format
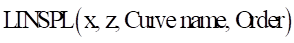
Arguments definition
|
|
An input variable for the LINSPL function •Generally, this variable is time or a function that returns a real number. |
|
|
An input variable for the LINSPL function •The second variable is necessary for three-dimensional spline functions. •This variable must be a function that returns a real number. Otherwise, 0 is applied. y1=f(x,z1), y2=f(x,z2) z1<z<z2 y = (z - z1) * (y2 – y1)/ (z2-z1) + y1 |
|
Curve name |
The name or argument number of the spline data defined by the subentity |
|
Order |
The interpolation method for the functions (return the value if 0, return calculation for 1st order differential equation if 1) dy1/dx = df(x,z1)/dx, dy2/dx = df(x,z2)/dx dy/dx = (z - z1) * (dy2/dx – dy1/dx)/ (z2-z1) + dy1/dx |
Formulation
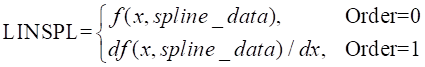
Example
LINSPL(time-1,0,1,0) <Argument: (1) Spline1>
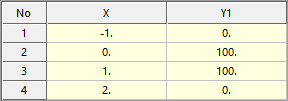
Figure 1 Spline Data
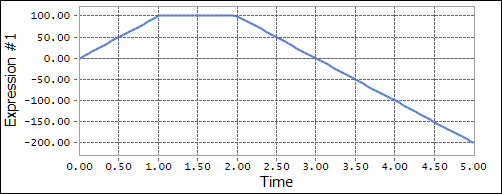
Figure 2 Example using the LINSPL function