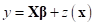
Kriging is a geostatistical method of spatial data interpolation. The mathematical model of kriging is named after D.G. Krige, who first introduced a version of this spatial prediction process. Kriging has been extensively described in the literature since Sacks et al. proposed the application of kriging in computer experiments.
Unlike the real tests, computer analysis codes are deterministic therefore it is not influenced with measurement errors. Hence, the approximate models can be defined as a combination of a regression model plus a departure term:
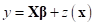
where,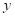 
is the approximate model, 
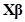is a polynomial type
regression model, and 
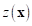is a Gaussian random process with
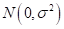. If the regression model 
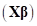globally approximates the
design space, the departure term 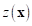represents the localized deviations
so that the Kriging model interpolates the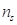 
sampled points.
The covariance matrix of 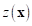is given by
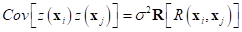
where,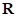 
is the correlation matrix and 
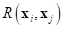is the correlation function
between any two of the 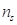sampled points. Hence, 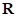is a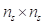 
symmetric matrix with ones in the
diagonal term. There are many correlation functions 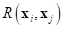. Among them, the Gaussian type is widely
used
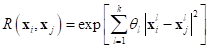
where,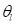 
are the unknown correlation
parameters to fit model. The estimates,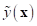 
of the response 
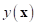at the untried values of 
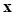are given by
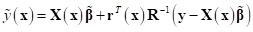
The correlation vector between 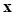and the sampled points 
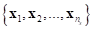is given by:
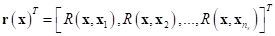
In the estimates, the unknown coefficients of regression model is determined as
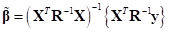
Also, in order to determine the unknown correlation
parameters 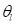, the estimate of
the variance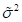 
(not the
variance in the observed data)
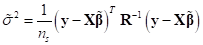
is introduced. Hence, the correction parameters 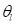is determined by solving
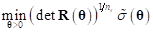or
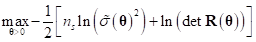
While any values for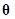 
create an interpolation model, the
best kriging model is found by solving the k-dimensional unconstrained
optimization problems described in the above.
Reference
1. Matheron G. Principles of geostatistics, Economic Geology 1963; 58:1246-1266.
2. Sacks J, Welch WJ, Mitchell TJ, Wynn HP, Design and analysis of computer experiments. Statistical Science 1989; 4:409-435.
3. Sacks J, Susannah SB, Welch WJ. Design for computer experiments. Technometrics 1989; 31:41-47