Friction defines the friction of Contact. And the user can also define the type as the following table.
|
Friction Type |
Entities |
|
Sliding and Stiction Type |
Element Assembly |
|
2D Segment Assembly | |
|
Sliding Type |
Segment Assembly |
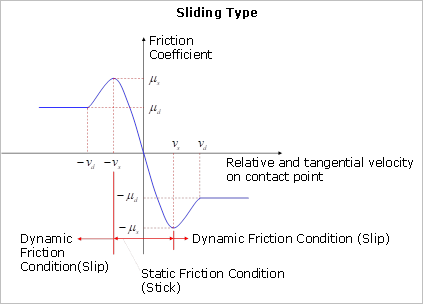
Friction type can be selected. The default value is sliding type. The difference between them is shown in Figure 1, 2 and Table 1


Figure 1 Sliding Type
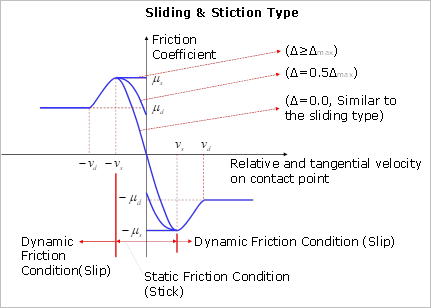
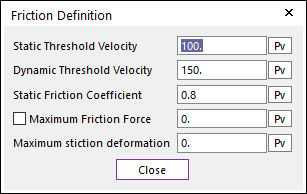
Figure 2 Sliding & Stiction Type
•Static Threshold Velocity ( ): This value is a criterion between
static and dynamic friction. If the relative velocity is less than this value,
the friction is on static friction. If not, the friction is on dynamic friction.
The friction coefficient of static friction region is calculated from following
equation for the sliding type. The mathematical definitions of all friction
types are defined in Table1.
): This value is a criterion between
static and dynamic friction. If the relative velocity is less than this value,
the friction is on static friction. If not, the friction is on dynamic friction.
The friction coefficient of static friction region is calculated from following
equation for the sliding type. The mathematical definitions of all friction
types are defined in Table1.
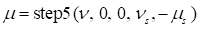
•Dynamic Threshold Velocity (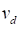 ): If the relative velocity between a
contact pair is greater than this value, the friction coefficient is same as the
specified dynamic friction coefficient. If the relative velocity between a
contact pair is greater than “Static Threshold Velocity” and less than
this value, the friction coefficient is defined as following. The detail
mathematical definitions is defined in Table1.
): If the relative velocity between a
contact pair is greater than this value, the friction coefficient is same as the
specified dynamic friction coefficient. If the relative velocity between a
contact pair is greater than “Static Threshold Velocity” and less than
this value, the friction coefficient is defined as following. The detail
mathematical definitions is defined in Table1.
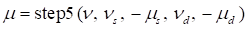
•Static Friction Coefficient (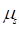 ): Specifies a static friction
coefficient.
): Specifies a static friction
coefficient.
•Maximum Friction Force (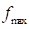 ): If this is checked, the contact
friction force is limited to this value.
): If this is checked, the contact
friction force is limited to this value.
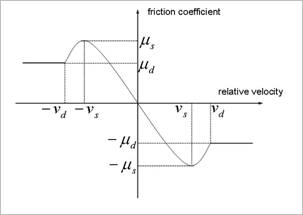
Figure 3 Relationship between relative velocity and friction coefficient in the sliding friction type
The friction force of contact entities is determined by the following equations.
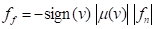
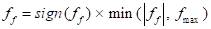
where, the 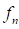 ,
, 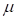 and
and 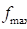 are the contact normal force,
the friction coefficient and the maximum friction force, respectively. The
friction coefficient of
are the contact normal force,
the friction coefficient and the maximum friction force, respectively. The
friction coefficient of 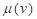 is determined by a relative and
tangential velocity on the contact point.
is determined by a relative and
tangential velocity on the contact point.
|
Type |
Sliding |
Sliding & Stiction |
|
Static friction condition ( |
|
|
|
Mathematical definition for Static friction condition |
|
|
|
Note1) |
In steady state, the slip is constant. Because, the
friction force is function of relative and tangential velocity ( |
In steady state, the slip is almost zero. Because, creep generate the stiction friction force for a stick effect. |
|
Note2) Mathematical definition for Dynamic friction condition |
| |
Table 1 Comparison in inclined plane model
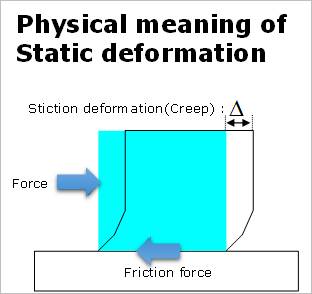
•Maximum Stiction Deformation: This controls the stick-slip effect on the contact. The value must be greater than or equal to zero. If the tangential velocity is smaller than the static threshold velocity, then the stick effect can be occurred. On the other hand, if the tangential velocity is greater than the static threshold velocity, then the friction model is on the slip condition.
Note
The friction coefficient of Sliding & Stiction Type is
function of relative velocity and creep (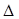 ) while the friction coefficient of
Sliding Type is function of relative velocity.
) while the friction coefficient of
Sliding Type is function of relative velocity.