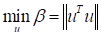
The mathematical formulation, for Reliability Index Analysis(RIA), is simplified to find the minimum distance to the limit state function in the standard normal variable space.
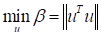
subject to
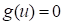
This formulation is developed by Hasofer and Lind, which has been referred to as AFOSM (Advanced First-Order Second Moment) method that overcomes the lack of invariance of MVFOSM.
There are many algorithms available that can solve this problem, such as mathematical optimization methods or other iteration algorithms. In the literature, several constrained optimization methods are used to solve the problem directly, which include primal optimization methods (Method of Feasible Directions, Gradient Projection and Generalized Reduced Gradient) and transformation methods (Penalty Function and Augmented Lagrange Multiplier). Each method has its advantages and disadvantages, depending upon the characteristic of the algorithm and the nature of the problem.
Unlike the optimization methods, another approach is the iteration algorithm. The currently used iteration method is HL-RF (Hasofer, Lind, Rackwits and Fiessler) method, which was originally proposed by Hasofer and Lind for second-moment reliability analysis and later extended by Rackwitz and Fiessler to include random variable distribution information.
The HL-RF method approximates the hyper-surface
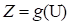by its tangent plane
at the most probable
point (MPP) 
, and then an
improved point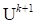 
is
obtained by computing the shortest distance from the approximate hyper-surface
to the origin. The
recurrence formula for 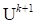is expressed as follows:
When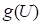 
is nonlinear function, the iterative
solution 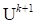is only
approximate. Thus, the above formula is applied repeatedly until the sequence
converges to the
minimum distance point. The HL-RF method has the advantage over the
optimization methods in that it is simple and faster. However, this method does
not guarantee the global convergence.
Recently, in order to reduce the computational burden of the
mathematical optimization method, the sequential approximate optimization
(SAO) method has been applied to solve the original RIA problem,
which solved the following approximate optimization problem until the sequence
converges to the
minimum distance point.
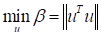
subject to
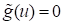
in which the limit state function is approximate by using the gradient information and function information. When the gradient information is available, two-point methods, widely used in structural optimization, are widely used. Otherwise, the meta-modeling methods including RSM are newly tried.