
All fatigue influencing factors have affected on the fatigue results according to selecting life criteria.
Effect on Stress Life Equation
Once a Stress-based Life is defined, all fatigue factors should be used to calculate the weighting factor(WF) so that new S-N relationship can be defined. So, the relation between the weighting factor(WF) and all fatigue influencing factors as following.

•WF : Weight Factor
•Kf : Stress Concentration Factor ( or Notch Factor Amp(Kt) )
( The Notch Factor Amp that is defined in Preferences must be treated as the Stress Concentration Factor when selected a stress life. )
•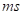 : Surface Factor
: Surface Factor
•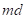 : Size Factor
: Size Factor
• : Load Factor
: Load Factor
• : Other Factor
: Other Factor
In the case of ‘Manson-Coffin’ stress life equation, Fuchs method that is shown in the Figure1 should be used in order to consider the weighting factor(WF) in stress life equation. That means that the first step is to calculate the stress amplitude at 106 reversals which should be divided by the weighting factor(WF). And then, the second step is to draw a line between the first point of the notched stress amplitude at 106 reversals and the second point of the un-notched stress amplitude at 103 reversals.
Therefore, the modified S-N curve can be reflected in the red line as shown in the Figure 1. At this point, the blue line is the original S-N curve without the defined fatigue factors.

Figure 1 Fuch method considering the stress concentration factor in Manson-Coffin stress life equation.
In the case of ‘ASME’ stress life equation, the stress concentration factor is multiplied with stress amplitude. The updated stress amplitude is used for evaluating fatigue life as new stress amplitude.
Effect on Strain Life Equation
Among several the fatigue influencing factors, just only the Notch Factor Amplitude(Kt) can affect the strain life equation. Therefore, unlike the stress life equation, the surface, size, load and other factor are useless when drawing the S-N curve for the strain life equation. At that time, the Neuber’s rule shown as the following equation should be used in order to consider the notch factor amplitude in the strain life equation.
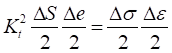
•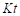 :
Notch Factor Amp.
:
Notch Factor Amp.
• : Nominal stress amplitude
: Nominal stress amplitude
•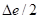 : Nominal strain amplitude
: Nominal strain amplitude
•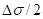 : Local stress amplitude
: Local stress amplitude
•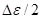 : Local strain amplitude
: Local strain amplitude
Where, both the nominal stress and the strain amplitude are not affected by the notch. On the contrary, both the local stress and strain amplitude are affected by the notch. In order to calculate both the local stress amplitude and the local strain amplitude, Ramberg-Osgood relation should be applied to as well as Neuber’s rule. The Ramberg-Osgood equation is the most commonly used cyclic stress-strain relation for fatigue analysis. The total strain is the sum of the elastic and plastic strains, which can be written as:
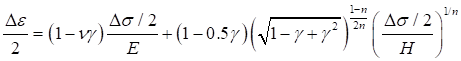
•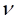 : Poisson’s ratio
: Poisson’s ratio
•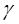 : Stress Biaxial
ratio
: Stress Biaxial
ratio
•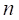 : Strain hardening
coefficient
: Strain hardening
coefficient
•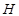 : cyclic strength
coefficient
: cyclic strength
coefficient
•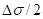 : Local stress amplitude
: Local stress amplitude
•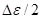 : Local strain amplitude
: Local strain amplitude
The first step is to obtain the nominal stress amplitude by using the Ramberg-Osgood relation from the given nominal strain amplitude. And then, because two factors such as the nominal stress amplitude and the nominal strain amplitude have known and the relation of both the local stress amplitude and the local strain amplitude is governed by the Ramberg-Osgood equation, the local strain amplitude can be obtained with easy by using the Newber’s rule.
Finally, the local strain is used for evaluating fatigue life in the defined strain life equation. But, Notch factor doesn’t have effect on evaluating fatigue life in the case of Max Shear Strain and Brown-Miller in strain life equation.
Effect on Safety Factor
When a Safety Factor is chosen, all fatigue factors should be used to calculate the weighting factor(WF). And then, it is multiplied with the given stress amplitude as following relation. Therefore, the modified stress amplitude should be applied to calculating the safety factor.
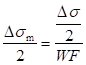
•WF : Weight Factor
•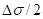 : Stress amplitude
: Stress amplitude
•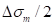 : Modified stress amplitude
: Modified stress amplitude