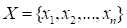 is known. Then,
the component
is known. Then,
the component  is
dependent and continuous for the probability density function
is
dependent and continuous for the probability density function 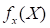 and the probability distribution
function
and the probability distribution
function 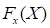 . Also, it is
assumed that the limit state function
. Also, it is
assumed that the limit state function
Suppose that the statistical distribution for random variable
vector, 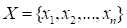 is known. Then,
the component
is known. Then,
the component  is
dependent and continuous for the probability density function
is
dependent and continuous for the probability density function 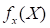 and the probability distribution
function
and the probability distribution
function 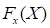 . Also, it is
assumed that the limit state function
. Also, it is
assumed that the limit state function
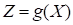
is a continuous function of 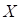 . Then, let’s define the probability of
failure as
. Then, let’s define the probability of
failure as
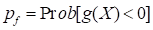
When the limit state function is linear, the probability of
failure can be exactly evaluated without the multiple integrations. For all
random variables  , let’s
consider that the mean value are
, let’s
consider that the mean value are 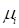 and the standard deviation are
and the standard deviation are 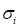 . Then, the normalized variable
. Then, the normalized variable
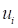 is defined by
is defined by
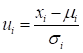
The probability of failure is given by
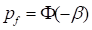
where 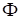 is ‘standard normal distribution
function’ and the safety factor
is ‘standard normal distribution
function’ and the safety factor  can be calculated from the geometric
relation shown in Figure 1. The safety factor
can be calculated from the geometric
relation shown in Figure 1. The safety factor  can be called as ‘Reliability
Index’. Suppose that the linear limit state function is
can be called as ‘Reliability
Index’. Suppose that the linear limit state function is 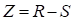 . Also, it is assumed that
. Also, it is assumed that 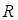 and
and 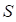 are normal distributions. Then, the
reliability index is denoted as
are normal distributions. Then, the
reliability index is denoted as
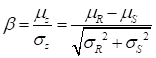
which is referred to as FOSM (First-Order Second Moment) method or MVFOSM (Mean Value First-Order Second-Moment) method.
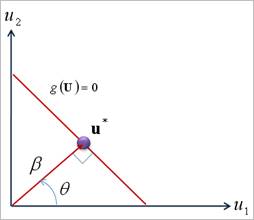
Figure 1 The Safety Index for Linear Limit State Function
In order to extend the above concept to the general probabilistic distribution, the equivalent normalization concept is introduced. This uses transformation matrix to change the random variables into the equivalently normalized variables.
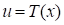 or
or
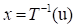
where 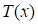 depends on the distribution of
depends on the distribution of 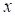 . In the standard normal variable
space shown in Figure 1, the probabilistic density function is decreased
exponentially from the origin. Thus, the probability of failure
. In the standard normal variable
space shown in Figure 1, the probabilistic density function is decreased
exponentially from the origin. Thus, the probability of failure 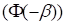 can be easily evaluated by obtaining
the minimum distance(
can be easily evaluated by obtaining
the minimum distance( ) from
the origin to the tangent plane of limit state function, which is graphically
explained in Figure 2.
) from
the origin to the tangent plane of limit state function, which is graphically
explained in Figure 2.
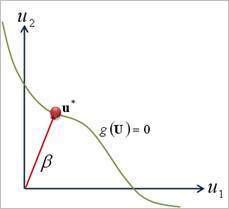
Figure 2 Graphical Representation of Reliability Index Analysis (RIA)