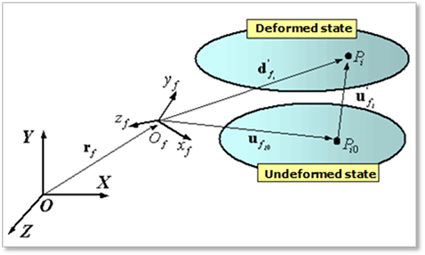
Figure 1 Configuration of a flexible body
Figure 1 shows the configuration of a flexible body f in the undeformed and deformed state. In the figure,
•XYZ : Inertia reference frame
•O : Origin of XYZ
•
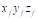: Flexible body
reference frame
•
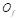:Origin of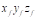 
•
: Node i in the undeformed state
•
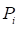: Node i in the deformed state
•
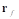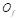
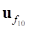: Position vector from the point O to the point
•
:
Position vector from the point 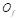to the
•
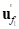: Nodal elastic deformation position vector from the point to the 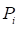measured with respect to 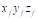. 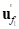is nodal elastic deformation
•
: 
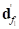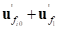, position vector from the point
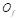to the point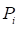
For a generic node 
of a flexible body 
, position vector of the node can be
written as
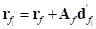(1)
where,
(2)
In above equation, 
is the translational modal
matrix of a node .
By taking time differentiation of the position vector,
velocity of the node is obtained as follows;
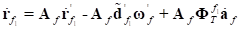(3)
By taking time differentiation of the velocity vector,
acceleration of the node is obtained as follows;
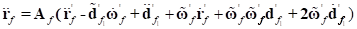(4)
Where,
(5)
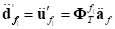(6)
EOM
By the virtual work principle, equations of motion can be obtained as
where,
