Effect Analysis
An effect will be said to be estimable if, and only if, there
is a contrast in the data which has for its expectation the particular effect
biased only by other effects which we choose to suppress. Experimental designs
in which main effects are aliased with each other are of no interest. Hence, it
is noted that the resolution of experimental designs is very important in the
effect analysis process.
Considering 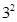 full factorial design, this
experiment has 1 degree-of-freedom for the main effects on factors A and B
full factorial design, this
experiment has 1 degree-of-freedom for the main effects on factors A and B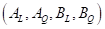 and 4 degree-of-freedom for the
two-factor interaction AB
and 4 degree-of-freedom for the
two-factor interaction AB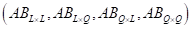 .
Hence, this design clearly estimates the main effects and two-factor interaction
effect.
.
Hence, this design clearly estimates the main effects and two-factor interaction
effect.
Now, let’s consider the fractional factorial design of 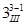 with
with 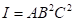 . The aliasing effects can be easily
determined by multiplying
. The aliasing effects can be easily
determined by multiplying 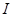 and
and
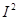 by effects.
by effects.

These relations show that the 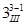 design will estimate the aliased
effects such as
design will estimate the aliased
effects such as 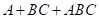 ,
, 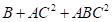 ,
, 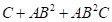 and
and 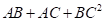 . From the definition of the Resolution
III,
. From the definition of the Resolution
III, 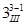 design should be
used when the main effects are nearly independent from two-factor or higher
effects in the system.
design should be
used when the main effects are nearly independent from two-factor or higher
effects in the system.
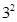 full factorial design, this
experiment has 1 degree-of-freedom for the main effects on factors A and B
full factorial design, this
experiment has 1 degree-of-freedom for the main effects on factors A and B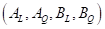 and 4 degree-of-freedom for the
two-factor interaction AB
and 4 degree-of-freedom for the
two-factor interaction AB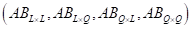 .
Hence, this design clearly estimates the main effects and two-factor interaction
effect.
.
Hence, this design clearly estimates the main effects and two-factor interaction
effect.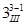 with
with 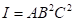 . The aliasing effects can be easily
determined by multiplying
. The aliasing effects can be easily
determined by multiplying 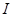 and
and
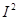 by effects.
by effects.
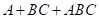 ,
, 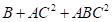 ,
, 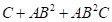 and
and 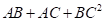 . From the definition of the Resolution
III,
. From the definition of the Resolution
III,