
Let’s reconsider the three-ball contact problem. The design constraint requires that the red ball should be contacted with the yellow ball. How can you formulate the contact between the red and the yellow balls? One case can be defined as “making the contact force to be greater than zero”. Another case is maintaining the minimum distance between two balls less than the sum of their radii. Both cases have some numerical problems. First, the minimum distance concept includes the numerical noise due to variable time steps. However, in this case, this noise will be relatively minimized because two balls will be contacted. Nevertheless, the same noise will be occurred when some design changes make no contact. Second, the contact force gives discontinuity during optimization process. If some design changes make no contact, the contact forces are zero. From the viewpoint of optimization process, the discontinuity is worse than the noise. So, the formulation of constraints “the red ball should be contacted with the yellow ball” is recommended to “the minimum distance between two balls should be less than the sum of their radii”.
If you check the non-linearity or discontinuity of performance, it is recommended that you use “Design Study”. Figure 2-4 shows the design study results. Figure 2-4(a) shows the distance between red ball and yellow ball. Figure 2-4(b) shows the contact force between both balls. In this comparison, we use “Bose’s Orthogonal Design” which is one of strength-II orthogonal array. Distance shows all values for ten levels but contact force does not. Why? They don’t exist when contact does not is occurred. So, distance value is recommended to represent the contact constraints between two balls

(a) Distance between red ball and yellow ball
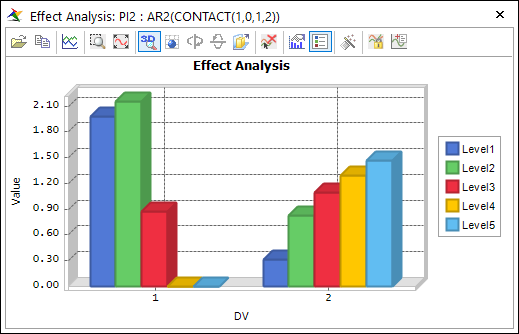
(b) Contact force between both balls
Figure 1 Effect analysis results by using “Design Study”