
Recently, the univariate dimension reduction methods (DRM) are newly presented, which can solve highly nonlinear reliability problems more accurately or more efficiently than FORM/SORM and Monte Carlo simulation methods. A major advantage of these decomposition methods so far based on the mean value points or MPP as reference points, over FORM/SORM is that higher-order approximations of performance functions can be achieved using function values only.

Figure 1 Limit Function Approximations by Various Methods
The transformed limit state functions 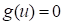 and
and 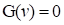 are the maps of the original limit
state function
are the maps of the original limit
state function 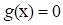 in the
standard Gaussian space (u space) and the rotated Gaussian space (v
space), respectively, as shown in Figure 1. The nearest point on the limit-state
surface to the origin, denoted by the MPP (
in the
standard Gaussian space (u space) and the rotated Gaussian space (v
space), respectively, as shown in Figure 1. The nearest point on the limit-state
surface to the origin, denoted by the MPP (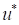 or
or 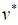 ) or beta point, has a distance
) or beta point, has a distance 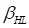 , which is commonly referred to as
the Hasofer-Lind reliability index. The determination of MPP and
, which is commonly referred to as
the Hasofer-Lind reliability index. The determination of MPP and
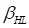 involves, based on
FORM, standard nonlinear constrained optimization and is usually
performed in the standard Gaussian space.
involves, based on
FORM, standard nonlinear constrained optimization and is usually
performed in the standard Gaussian space.
Consider a univariate approximation of 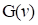 , denoted by
, denoted by
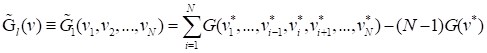
where each term in the summation is a function of only one
variable. As higher-order univariate terms can be included in the approximation,
the univariate approximation may be more accurate than FORM and
SORM. In addition to the MPFP as the chosen reference point, the
accuracy of the univariate approximation may depend on the orientation of the
first  axes. In general,
a Gram-Schmidt orthogonalization is used to determine the transformation
matrix.
axes. In general,
a Gram-Schmidt orthogonalization is used to determine the transformation
matrix.
Finally, the failure probability is approximated by
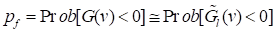
The univariate integration can be evaluated easily by standard one-dimensional Gauss-Hermite numerical quadrature. The decomposition method involving univariate approximation and univariate integration is referred to as the MPP-based Dimension Reduction Method (MPP-based DRM).