DIF

The DIF function returns the integral calculation for the differential equation in a differential equation entity.

Format

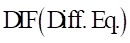
Arguments definition

Formulation

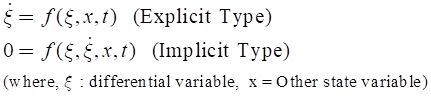
Example

DIF(Model1.DE1)

DIF(1) <Argument: (1)DE1>

Figure 1  Example of using the DIF function

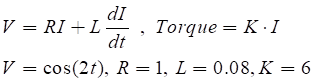
An explicit differential equation can be used to create a torque model for the electrical motor described above.

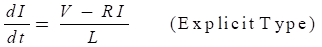
To define the explicit differential equation above:

Create a parametric value for each coefficient (R,L,K), and build models for the body, revolute joint, and rotational axial force. The result is derived by running the organized differential equation through the expression and DIF and applying each entity through the Rotational Axial Force model.

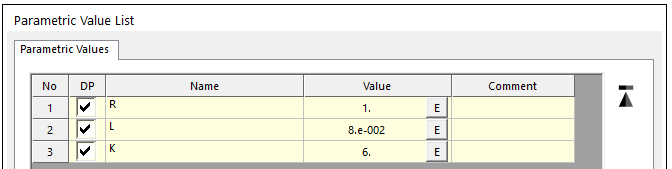
1.  Create Parametric Value for each values of R, L, K.

2.  Create Cylinder Body, Revolute Joint and Rotational Axial Force step by step.

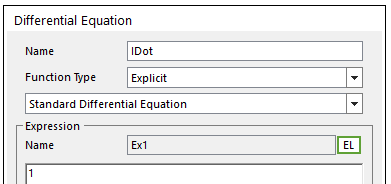
3.  Create a dummy differential equation.

•     Name: IDot

•     Function Type: Explicit

•     Expression: 1

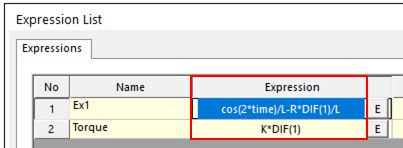
4.  Create above two equations as expression.

•     Torque: K*DIF(1) <Argument: (1) IDot>

•     EX1: cos(2*time)/L-R*DIF(1)/L <Argument: (1) IDot>

5.  Change the IDot of expression Ex1 to EX1.

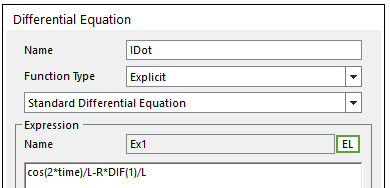
6.  Simulate an example model.

7.  Check result

Plot > Model Database > DifferentialEq > IDot > DIF, DIF1

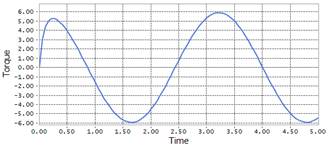
Figure 2  Result of using the DIF function