
MTT2D assumes that the depth of the model is a length unit. This depth assumption applies to all MTT2D entities, including the:
•Sheet
•Rollers
•Guides
Input parameters should be set to reflect the average effect of that entity over a strip of the sheet that is a length unit in width.
Description of MTT2D Example Model
For example, consider a model that is similar to the tutorial model included in this section (see Figure below). It includes an A4-sized sheet (200 mm by 300mm) that is being fed sideways through two roller pairs (nips). The length unit for the model is millimeters (mm). The other units of the model are:
•Kilograms (kg)
•Newtons (N)
•Seconds (sec)
The length of the sheet that is fed through the nips is 200 mm. It is modeled with 20 segments that are 10 mm in length.

Figure 1 Sample MTT2D Model
Sheet Definition
The fact that the sheet has a depth of 300 mm does not apply to this model. Rather it is helpful for the user to visualize the sheet as being a slender strip that is:
•200 mm in length
•1 mm in depth
Consider the properties entered in the Sheet dialog box below:
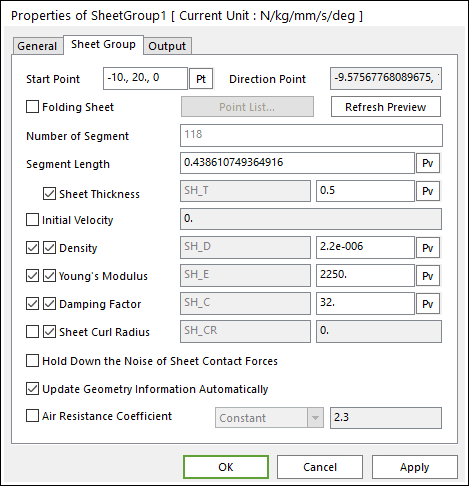
Figure 1 Properties of SheetGroup dialog box
•Properties are Not Dependent on 2D Assumptions
The first six values (Sheet Start Point and Direction Point, Numbers of Segments, Sheet Segment Length, Sheet Thickness and Initial Velocity) are set according the standard physical properties of the sheet. The Young’s Modulus is the standard property and depends upon the material of the sheet. The structural damping (Sheet C) of the sheet and the Sheet Curl are properties of the material that are not dependent upon any 2D assumptions.
•Setting the Correct Paper Density
The next property, Density, is a 2D density based upon the presented area of the sheet in the 2D model. In this example, each sheet has a mass of 66 grams (0.066 kg). The thickness of the sheet is 0.5 mm and its volume is 30,000 mm3. Therefore, the volume density is 2.2e-03 g/mm3 (2.2e-06 kg/mm3). Since the depth of the sheet is 1 mm, the area density is 2.2e-03 g/mm2 (2.2e-06 kg/mm2).
Roller Definition
It is typical to have several (from 2 to 5 or more) sets of rollers at each location. They are distributed in order to prevent 3D effects such as skewing and buckling. The simulation of 2D models does not consider such effects, so it is sufficient to consider the average effect of the rollers on the paper.
•Determining Average Roller Mass and Inertia
For example, consider 3 sets of rollers with locations distributed across the depth of our sheet. Each driving roller has a:
•Mass of 0.225 kg (225 grams)
•Rotational inertia of 3.9 kg-mm2
•Width of 12 mm
The user determines the correct mass value for the driving roller by summing the masses of all of the rollers and dividing by the ratio of the paper depth to the length unit. In this case the total roller mass is 0.675 kg, so the roller mass should be set to be 0.00225 kg (0.675/300). The inertia value is scaled in the same way since the 2D dimensions do not change. The correct inertia value to use is 0.013 kg-mm2.
•Determining Average Nip Spring Parameters
The nip spring parameters are set in a similar way. The spring rates, damping rates and preloads are added together and then divided by the ratio of the paper depth to the length unit. For example, with 3 movable rollers with spring rates of 0.1 N/mm each, the nip spring stiffness should be set to 0.001 N/mm (0.1 x 3 / 300).
Contact Properties
There are several ways to approach the definition of contact properties. One way is to do experiments with the sheet to measure the contact forces under various conditions. Another approach it to define the properties based upon fundamental material characteristics. The data obtained at the sheet level must be scaled down to provide the portion of the total force that is appropriate for a sheet that is only one length unit in depth.
•Determining Average Contact Parameters
For example, the contact stiffness between the roller and the sheet should be divided by the ratio of the paper depth to the length unit. For example, there are 3 movable rollers with a contact stiffness of 120 N/mm to the sheet, the roller-to-sheet contact stiffness should be set to 1.2 N/mm (120 x 3 / 300). Since the roller force is similarly divided, the proper displacement will occur within the roller-sheet interaction. The same logic applies to the damping parameters.
•Using Material Properties to Determine Contact Parameters
Contact parameters may be derived from the material properties. Those values should be scaled appropriately to account for the reduced depth of the sheet.