In general, standard deviation is the best measure of process
or design variability because the smaller the standard deviation, the less
variability in them. If one can reduce sigma 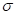 , to the point that the specifications are
at
, to the point that the specifications are
at 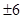 , then
, then 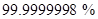 of the product or design will be
between specifications. Figure 1 shows the feasibility of both sided inequality
constraints. Suppose that three colored distributions have same center but
different sigma. If one distribution satisfies the relation of
of the product or design will be
between specifications. Figure 1 shows the feasibility of both sided inequality
constraints. Suppose that three colored distributions have same center but
different sigma. If one distribution satisfies the relation of 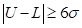 , then we say that it satisfies 6-sigma constraints.
, then we say that it satisfies 6-sigma constraints.
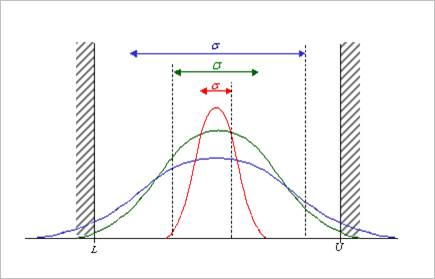
Figure 1 Feasibility of several distributions with same
centers
In the practical design, the inequality constraints have only
one-side limitation such as equation (4) in “Robust Design Optimization”.
Figure 2 shows the feasibility of several distributions with shifted centers. If
you change the design variables  , the mean and variance of a performance
, the mean and variance of a performance
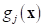 will be changed, even
though all design variables have same variations
will be changed, even
though all design variables have same variations 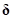 .
.
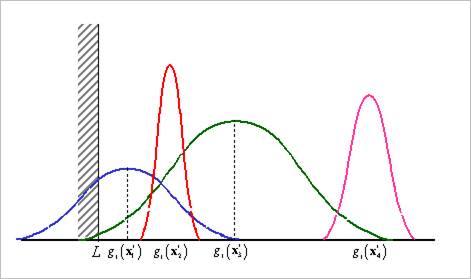
Figure 2 Feasibility of several distributions with
shifted centers
Next, the definition method of 6-sigma is explained. In the
Robust Design Optimization window, PI should be defined as
Constraint. Then, its goal is selected from LE or GE types.
In the following figure, Nip spring force is selected as LE type constraint.
Also, its value should be less than 10. The robust index is defined as “1”. In
AutoDesign, this inequality constraint is represented as:
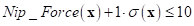

If one defines the robust index as “6”, then the nip force
constraint is 6-sigma constraint as
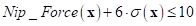 .
.
As you define the robust index between 0 ~ 6, the percent
feasibility will be changed. Table 1 shows the percent between robust index and
the feasibility of inequality constraints.
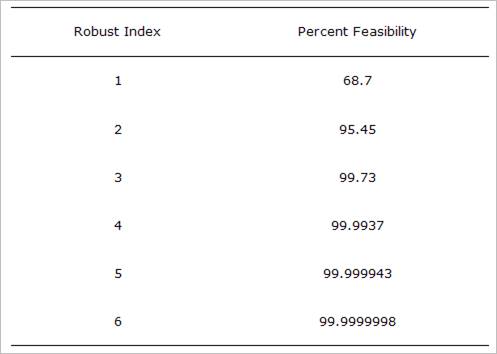
Table 1 Percent feasibility for robust formulation
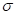 , to the point that the specifications are
at
, to the point that the specifications are
at 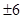 , then
, then 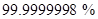 of the product or design will be
between specifications. Figure 1 shows the feasibility of both sided inequality
constraints. Suppose that three colored distributions have same center but
different sigma. If one distribution satisfies the relation of
of the product or design will be
between specifications. Figure 1 shows the feasibility of both sided inequality
constraints. Suppose that three colored distributions have same center but
different sigma. If one distribution satisfies the relation of 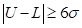 , then we say that it satisfies 6-sigma constraints.
, then we say that it satisfies 6-sigma constraints.
 , the mean and variance of a performance
, the mean and variance of a performance
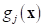 will be changed, even
though all design variables have same variations
will be changed, even
though all design variables have same variations 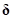 .
.
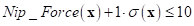

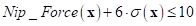 .
.