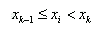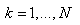(
),
Interpolation helps you perform one-dimensional interpolation of the values in a curve to create an evenly spaced sampling of the curve values.
Linear
Use the first order Lagrange’s formula. The equations of linear interpolation are defined as,
If ( ),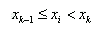
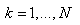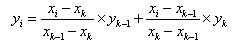
Here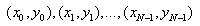 
are N points in curve data, 
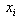is the point at which to interpolate
and is defined by interpolation region and the number of interpolated value,
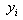is the interpolated value.
Polynomial
Through any two points there is a unique line. Through any
three points, a unique quadratic. The interpolating polynomial of degree N-1
through the N points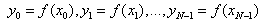 
is given explicitly by Lagrange’s
classical formula,
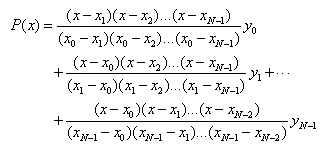
There are N terms, each a polynomial of degree N-1 and each
constructed to be zero at all of the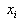
except one, at which it is constructed to
be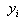 
. A using algorithm (for constructing the
same, unique, interpolating polynomial) is Neville’s algorithm.
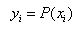
Here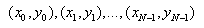 
are N points in curve data,
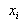is the point at which to interpolate
and is defined by interpolation region and the number of interpolated value,
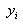is the interpolated value.
•2-order Polynomial makes Polynomial function using first 3 points in turn. The equations of 2-order polynomial interpolation are defined as,
If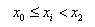 
,
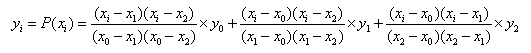
If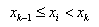 
( 
),
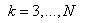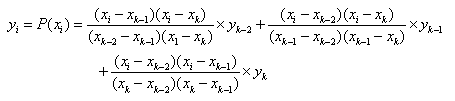
•3-order Polynomial makes Polynomial function using first 4 points in turn. The equations of 3-order polynomial interpolation are defined as,
If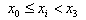 
,
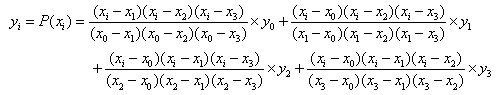
If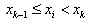 
( 
),
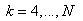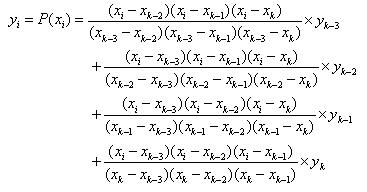
Akima
The Akima interpolation is similar to the Hermite interpolation. Derivatives at nodes are calculated in the Akima interpolation, but derivatives at nodes are prescribed in the Hermite interpolation.
•Polynomial
Let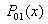 
be an interpolation function at x (
)
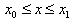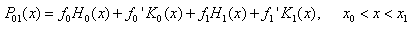where,
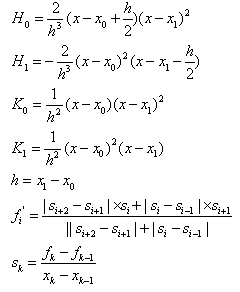
•Initial and End points condition
The calculations
of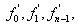 
and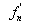 
using Eq.( ) are
impossible since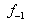 
and 
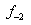are needed to calculate
, 
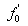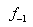is needed to calculate
, 
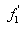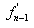and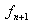 
is needed to calculate 
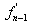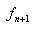and 
and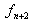 
are needed to calculate 
.
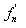Let an interpolation function f(x) be expressed as
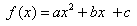
for points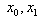 
,
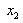and
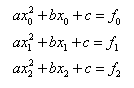or
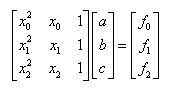
By solving the
above equation a, b, and c can be obtained. Derivation of Eq.( ) with respect to
x gives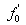 
and 
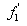as
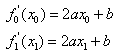
CSpline(Cubic Spline)
The cubic spline interpolation is to get an interpolation
formula that is smooth in the first derivative, and continuous in the second
derivative, both within an interval and at its boundaries. Given a tabulated
function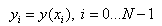
, focus attention on particular interval,
between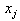 
and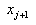 
. The cubic
spline interpolation in that interval gives the interpolation formula
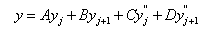
where,
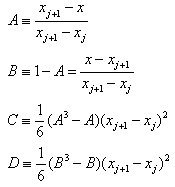
The key idea of a cubic spline is to require the continuity
between two intervals and to use it to get equations for the second
derivatives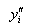
. For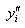 
the following equations
are obtained
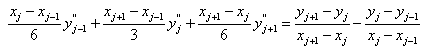
These are N-2 linear equations in the N unknowns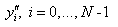 
. For a unique solution, two further
conditions are needed. For computing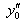 
and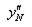 
, initial and end
conditions are used. The equation for points 
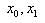and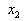 
are expressed as
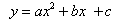
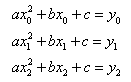or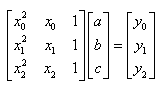 
By solving the above equation a, b, and c can be obtained.
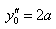
As same,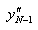 
is obtained by end condition.