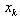 of input points and produces a
sequence
of input points and produces a
sequence 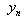 of output points by the formula
of output points by the formula
You can filter curve data to remove or emphasize the specific region of time signal. Two methods are supplied for filtering. One is a transfer function. The other is a Butterworth filer.
Transfer function
Directly specifies the coefficients of transfer function.
Butterworth filter
Computes the coefficients of a transfer function by Butterworth filter algorithm. The Butterworth approximation and bilinear transform are used to obtain transfer function of filter.
Digital Filter
The filter of RecurDyn/Plot is a digital filer. The
most general filter takes a sequence 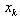 of input points and produces a
sequence
of input points and produces a
sequence 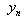 of output points by the formula
of output points by the formula
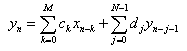
Here the M+1 coefficients 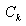 and the N coefficients
and the N coefficients
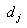 are fixed and define the filter
response. The filter produces each new output value from the current and M
previous input values, and from its own N previous output values. If N=0, so
that there is no second sum, then the filter is called nonrecursive or finite
impulse response (FIR). If , then it is called recursive or infinite impulse
response (IIR).
are fixed and define the filter
response. The filter produces each new output value from the current and M
previous input values, and from its own N previous output values. If N=0, so
that there is no second sum, then the filter is called nonrecursive or finite
impulse response (FIR). If , then it is called recursive or infinite impulse
response (IIR).
The relation between the 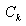 ’s and
’s and 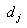 ’s and the filter response function
’s and the filter response function
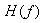 is
is
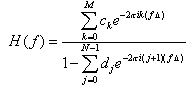
where  is, as usual, the sampling interval.
is, as usual, the sampling interval.
Taking Z transform, Transfer function 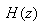 is
is
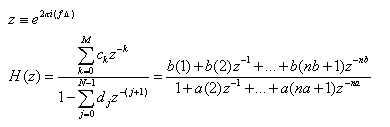
Here M equals to nb and N-1 equal to na.
The input-output description of this filtering operation in the Z-transform domain is a rational transfer function,
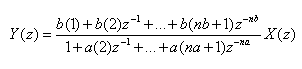
Design the digital filter
•Butterworth approximation
•Analog Lowpass Butterworth Filter Design
The magnitude-square response of an N-th order analog lowpass Butterworth filter is given by
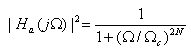
where 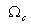 is called the cutoff frequency. The
first 2N-1 derivatives of
is called the cutoff frequency. The
first 2N-1 derivatives of 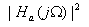 at
at 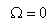 are equal to zero. The
Butterworth lowpass filter thus is said to have a maximally-flat
magnitude at
are equal to zero. The
Butterworth lowpass filter thus is said to have a maximally-flat
magnitude at 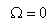 .
.
•Design of Analog Highpass , Bandpass and Bandstop Filter
RecurDyn/Plot performs the step of the next design process to obtain Highpass , Bandpass and Bandstop Filter.
Step 1 - Develop
of specifications of a prototype analog lowpass filter 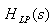 from
specifications of desired analog filter
from
specifications of desired analog filter 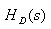 using a frequency
transformation
using a frequency
transformation
Step 2 - Design the prototype analog lowpass filter
Step 3 -
Determine the transfer function 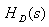 of desired analog
filter by applying the inverse frequency transformation to
of desired analog
filter by applying the inverse frequency transformation to 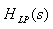 .
.
•Analog Highpass Butterworth Filter Design
Spectral Transformation of highpass filter is defined as,

where, 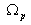 is the passband edge frequency of
is the passband edge frequency of
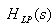 and
and 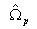 is the passband
edge frequency of
is the passband
edge frequency of 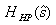 .
.
•Analog Bandpass Butterworth Design Filter
Spectral Transformation of bandpass filter is defined as,
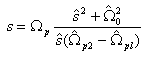
where, 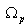 is the passbandedge frequency
of
is the passbandedge frequency
of 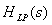 ,
,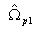 and
and 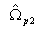 are the lower
and upper passband edge frequencies of desired bandpass filter
are the lower
and upper passband edge frequencies of desired bandpass filter 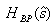 .
.
•Analog Bandstop Butterworth Design Filter
Spectral Transformation of bandstop filter is defined as,
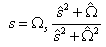
where 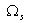 is the stopband edge frequency of
is the stopband edge frequency of
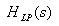 , and
, and 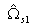 and
and 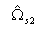 are the lower and upper stopbandedge
frequencies of the desired bandstop filter
are the lower and upper stopbandedge
frequencies of the desired bandstop filter 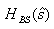 .
.
•Bilnear Transformation
Bilnear transformation makes digital filter from analog Butterworth filer. The bilinear transformation maps the s domain into the z domain by

where, 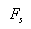 is the sampling frequency in
Herz.
is the sampling frequency in
Herz.