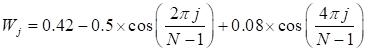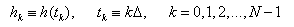
FFT(Fast Fourier Transform) is a mathematical algorithm that takes a time-domain data and maps it into its frequency-domain.
Discrete Fourier Transform
Suppose that we have N consecutive sampled values
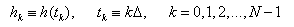
so that the sampling interval is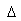 
. To make things
simpler, let us also suppose that N is even. With N numbers of input, we can
estimate the Fourier transform 
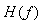at the discrete values.
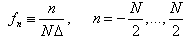
The extreme values of n correspond exactly to the lower and upper limits of the Nyquist critical frequency range.
The Fourier transform is approximated by a discrete sum. The discrete Fourier transform is obtained as,
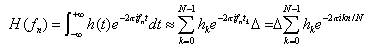
If the number of sampled values is an even power of two (for
example, 256, 512, 1024, and so on), the discrete Fourier transform can be
computed in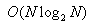 
operations with an algorithm
called the fast Fourier transform, or FFT.
•Magnitude
FFT/magnitude determines the magnitude (abs) of the complex value returned from the FFT algorithm.
•Phase
FFT/Phase determines the phase angle of the complex value returned from the standard FFT algorithm.
•Power Spectral Density (PSD)
FFT/Power Spectral Density determines the periodogram estimation of the complex value returned from the standard FFT algorithm. If we take an N point sample of the function c(t) at equal intervals and use the FFT to compute its discrete Fourier transform
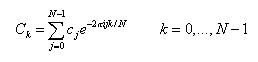
Then the periodogram estimate is defined at N/2+1 frequencies as
where, 
is defined only
for the zero and positive frequencies
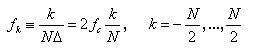
•Window Method
The time-domain data is assumed a periodic sample from a continuous, infinite series of data for FFT. Window methods are used to reduce discontinuities from mismatching start and end and ensure periodicity of the FFT conditions.
The functions of
window methods are defined below. In the equation,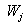 
is the function of the
window method and N is the number of sampled values.
•Square Window
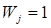
•Bartlett Widow
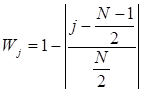
•Welch Window
•Hanning Window
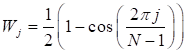
•Hamming Window
•Blackman
