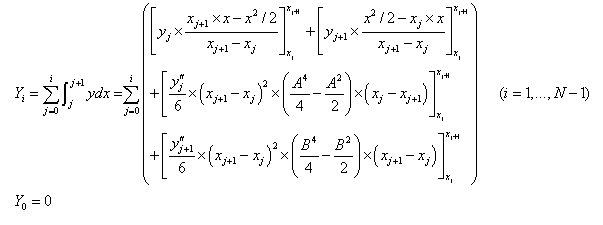are given. The differential of
points is defined as,
are given. The differential of
points is defined as,
Calculus helps you perform the deferential or integral function on the data in any curve.
Differential
Differential numerically differentiates the curve data.
•Linear
The N points  are given. The differential of
points is defined as,
are given. The differential of
points is defined as,
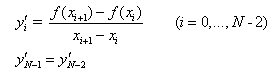
•Smooth
The smoothing
differential evaluates the derivative by fitting a Cspline(cubic spline) to the
curve data and analytically forming the derivative. Given a tabulated function
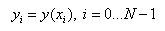 , focus attention on particular
interval, between
, focus attention on particular
interval, between 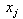 and
and 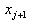 . The cubic
spline interpolation in that interval gives the interpolation formula
. The cubic
spline interpolation in that interval gives the interpolation formula 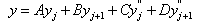 where,
where,
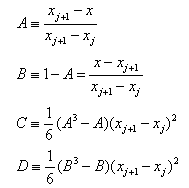
The first derivative of Cspline is obtained as,

Integral
Integral numerically integrates the curve data.
•Linear
The N points
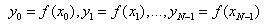 are given. The integral of points is
defined as,
are given. The integral of points is
defined as,
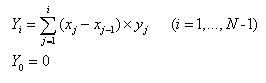
•Smooth
The smoothing
integral evaluates the integral by fitting a Cspline(cubic spline) to the curve
data and analytically forming the integral. Given a tabulated function 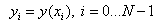 , focus attention on particular
interval, between
, focus attention on particular
interval, between 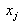 and
and 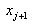 . The
cubic spline interpolation in that interval gives the interpolation formula
. The
cubic spline interpolation in that interval gives the interpolation formula
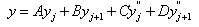 where,
where,

The integral of Cspline is obtained as,