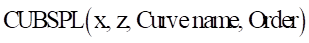
The CUBSPL function uses Cubic spline interpolation to return the y values for the x variable input through the spline entity. The cubic spline function’s 2nd order differential equation calculation is a curve. As such, it is suitable to use the spline input function for motion. It uses spline curve in x-y direction and linear interpolate in x-z direction. So, if the user wants to smooth surface effect then data set of z direction must be dense.
Format
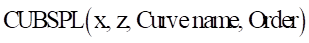
Arguments definition
|
|
An input variable for CUBSPL Generally, this variable is time or a function that returns a real number. |
|
|
An input variable for CUBSPL •This second variable is necessary for three-dimensional spline functions. •This variable must be a function that returns a real number. Otherwise, 0 is applied. y1=f(x,z1), y2=f(x,z2) z1<z<z2 y = (z - z1) * (y2 – y1)/ (z2-z1) + y1 |
|
Curve name |
The name or argument number for the spline data defined by the subentity |
|
Order |
The interpolation methods for the functions (return the value if 0, return calculation for 1st order differential equation if 1, and return calculation for 2nd order differential equation if 2) dy1/dx = df(x,z1)/dx, dy2/dx = df(x,z2)/dx dy/dx = (z - z1) * (dy2/dx – dy1/dx)/ (z2-z1) + dy1/dx |
Formulation
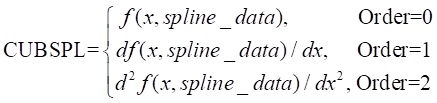
Example
CUBSPL(time,0,1,0) <Argument: (1) Spline1>
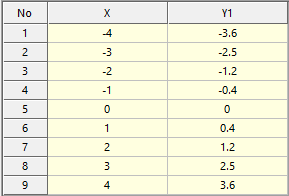
Figure 1 Spline Data
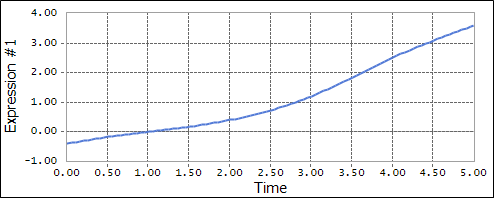
Figure 2 Example using the CUBSPL function