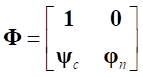
Component Mode Synthesis (CMS) is a well-known reduction method. And Craig-Bampton method[1] is another name of CMS. The Craig-Bampton mode is combination of a constraint mode and a fixed-interface normal mode.
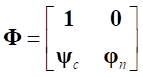
The first column is a constraint mode. And the last column is a fixed interface normal mode. Therefore, the number of CMS modes is (Interface DOFs + No. Fixed interface normal modes).
Constraint mode
The constraint mode is computed as the following condition.

Where, c means DOFs for interface nodes, n means the other DOFs except for interface nodes.
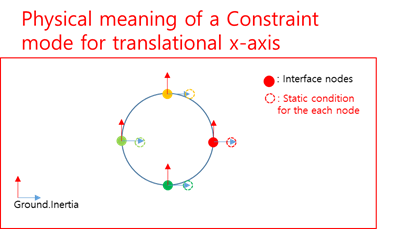
Figure 1 Physical meaning of a constraint mode
Constraint mode with a special coordinate system
The constraint mode is computed as the following condition.
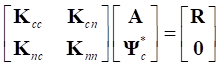
Where, c means DOFs for interface nodes, n means the other DOFs except for interface nodes. A means an orientation matrix (a matrix 3x3, and consist of direction cosine vectors).
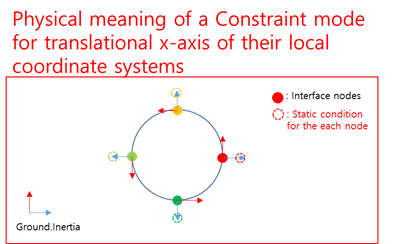
Figure 2 Physical meaning of a constraint mode with a special coordinate system
Fixed interface normal mode
The fixed interface normal mode is computed the following eigenvalue equation.
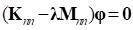
The computed eigenvectors must be following the condition called as the orthonormalization with the mass matrix.
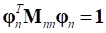
Orthonormalization
The Craig-Bampton mode is not directly used. Because, the
mode shape of RecurDyn/RFlex must be an orthonormalization with
the global mass matrix. A transformation matrix 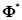 is needed for the
orthonormalization like following equation.
is needed for the
orthonormalization like following equation.
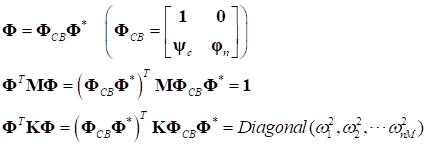
Reference,
[1] Craig R. R. and Bampton M. C. C., “Coupling of Substructures for Dynamic Analysis”, AIAA Journal, vol. 6, PP. 1313-1319., 1968