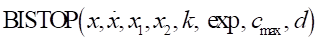
The BISTOP function returns the contact force of a model in a gap defined by the relative location and velocity of two markers.
Format
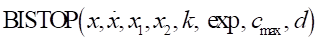
Arguments definition
|
Distance( |
The relative distance between the two markers on the contacting entities |
|
Velocity( |
The relative velocity between the two markers on the contacting entities |
|
Free
length1( |
The contact distance between the two markers on the contacting entities •This value must be a real number or a function that returns a real number. •The free length(x1) is used to determine whether or not contact is made. |
|
Free
length2( |
The contact distance between the two markers on the contacting entities •This value must be a real number or a function that returns a real number. •Free length(x2) is used to determine whether or not contact is made. |
|
Stiffness( |
The modulus rigidity on the spring force |
|
Stiffness
exponent( |
The nonlinear coefficient value on the surface of the spring force |
|
Damping( |
The maximum damping coefficient This must be a real number or a function that returns a real number |
|
Penetration( |
The depth of infiltration that induces the maximum damping coefficient |
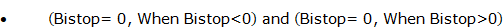
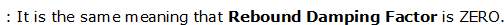
Formulation
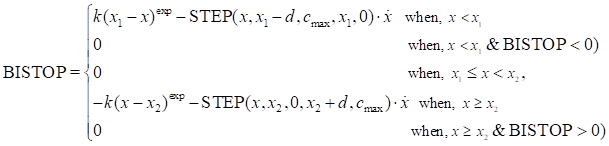
Example
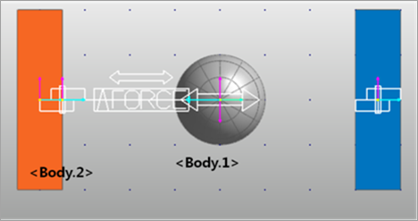
Figure 1 Example modeling for the BISTOP function
BISTOP(DX(Body1.Marker2,Body2.Marker1,Body2.Marker1),VX(Body1.Marker2,Body2.Marker1,Body2.Marker1),150,600,10000,1.3,100,2)
•x = DX: Distance variable
•
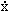= VX: Time derivative of x
•x1 = 150: Lower bound of x
•x2 = 600: Upper bound of x
•k = 10000: Stiffness
•exp = 1.3: Exponent of force
•cmax = 100: Maximum damping coefficient
•d = 2: Boundary penetration
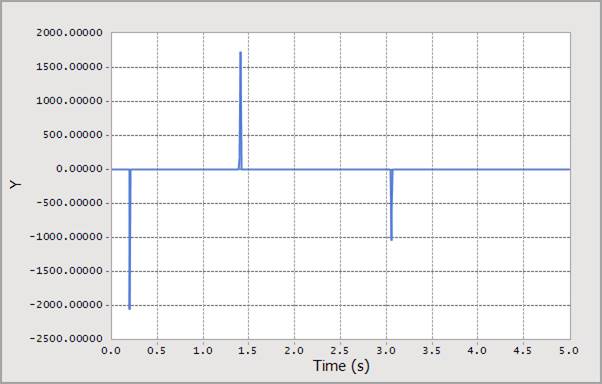
Figure 2 Scope result using the BISTOP function
