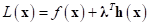
ALM method may be called as Method of Multiplier (MOM) or Primal-Dual Method. Let’s consider Lagrangian functional only for equality constraints.
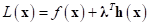
Now, for a Lagrange multiplier vector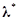 
, suppose that there is an optimum 
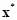for the following
unconstrained optimization problem.
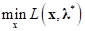
If 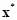satisfy all the equality constraints
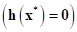in the original design
problem, 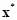is an optimum
for the original optimization problem and 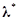is a Lagrange multiplier optimum.
Consequently, the original optimization problem can be transformed into the
following problem that have the same optimum 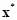and .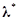
subject to 
In order to avoid the unboundness of Lagrangian, a penalty function is introduced. We call it as augmented Lagrangian.
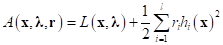
where,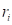 
is the penalty parameter for the ith
equality constraint. In the ALM method, the unconstrained optimization tool
sequentially minimize the augmented Lagrangian for the given value of
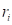and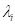 
. Then, these two parameters are modified
to satisfy the optimality condition.
The update rule for Lagrange multipliers can be determined from the following relation.
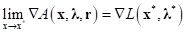
This implies
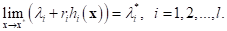
Hence, the update rule for Lagrange multipliers is
where, the superscript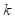 
is the iteration of ALM
algorithm.
Inequality constraints are transformed into equality
constraints by adding slack variables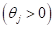 
. Thus, the augmented Lagrangian
becomes
.
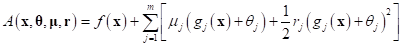Then, a new primal variables are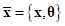 
. The augmented Lagrangian should
satisfy the optimality condition for slack variable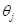 
.
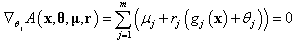
Hence, an optimum of slack variable 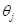is
.
Now, these optimum values are substituted into the originally transformed form.
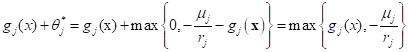
Hence, the augmented Lagrangian for inequality constraints are transformed into the following simple functional.
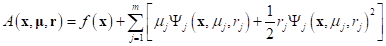
where,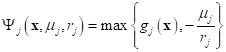 
.
Also, the Lagrange multiplier update rule is defined as
.
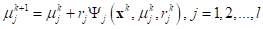In order to sequentially solve the augmented
Lagrangian, AutoDesign uses quasi-Newton(BFGS) for 
and conjugate gradient
method (Hestnes-Stiefel) for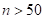 
.